题目内容
函数y=2x2+3在点P(1,5)的切线方程为: .
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,直线与圆
分析:欲求在点(1,5)处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
解答:
解:∵y=2x2+3,∴y′=4x,
∴x=1时,y′=4,
∴曲线y=2x2+3在点P(1,5)处的切线方程为:y-5=4×(x-1),即y=4x+1,
故答案为:4x-y+1=0.
∴x=1时,y′=4,
∴曲线y=2x2+3在点P(1,5)处的切线方程为:y-5=4×(x-1),即y=4x+1,
故答案为:4x-y+1=0.
点评:本题主要考查直线的斜率、直线的方程、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
边长为a的正方形ABCD沿对角线BD折成90°的二面角,则AC的长为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、a |
已知函数f(x)满足f(x+1)=
,且当x∈(0,1]时,f(x)=x,g(x)=m(x+3),若方程f(x)=g(x)在区间(-1,1]上有两个不同的实根,则实数m的取值范围是( )
| 1 |
| f(x)+1 |
A、(0,
| ||
B、(0,
| ||
C、(
| ||
D、(
|
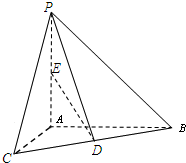 如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D、E分别是BC、AP的中点.求异面直线AC与ED所成的角的大小为
如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D、E分别是BC、AP的中点.求异面直线AC与ED所成的角的大小为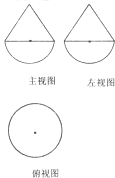 已知一个几何体是由上、下两部分构成的组合体,其三视图如图,若图中圆的半径为l,等腰三角形的腰长为
已知一个几何体是由上、下两部分构成的组合体,其三视图如图,若图中圆的半径为l,等腰三角形的腰长为