题目内容
11.函数f(x)=cos2x,x∈[$\frac{π}{6}$,$\frac{5π}{6}$]的值域是$[-1,\frac{1}{2}]$.分析 由已知可求2x的范围,利用余弦函数的图象和性质即可得解其值域.
解答 解:∵x∈[$\frac{π}{6}$,$\frac{5π}{6}$],
∴2x∈[$\frac{π}{3}$,$\frac{5π}{3}$],
∴f(x)=cos2x∈$[-1,\frac{1}{2}]$.
故答案为:$[-1,\frac{1}{2}]$
点评 本题主要考查了余弦函数的图象和性质的应用,属于基础题.

练习册系列答案
相关题目
2.用一个平面去截一个几何体,得到的截面不可能是圆的几何体是( )
| A. | 圆锥 | B. | 圆柱 | C. | 球 | D. | 三棱锥 |
19.已知集合A={x∈Z|(x+2)(x-1)<0},B={-2,-1},那么A∪B等于( )
| A. | {-2,-1,0,1} | B. | {-2,-1,0} | C. | {-2,-1} | D. | {-1} |
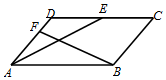 如图所示,在平行四边形ABCD中,AB=4,AD=3,E是边CD的中点,$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{DA}$,若$\overrightarrow{AE}$•$\overrightarrow{BF}$=-4,则sin∠BAD=$\frac{\sqrt{15}}{4}$.
如图所示,在平行四边形ABCD中,AB=4,AD=3,E是边CD的中点,$\overrightarrow{DF}$=$\frac{1}{3}$$\overrightarrow{DA}$,若$\overrightarrow{AE}$•$\overrightarrow{BF}$=-4,则sin∠BAD=$\frac{\sqrt{15}}{4}$.