题目内容
抛物线y2=-8x中，以（-1，1）为中点的弦所在的直线方程是（ ）
| A、x-4y-3=0 |
| B、x+4y+3=0 |
| C、4x+y-3=0 |
| D、4x+y+3=0 |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：先设出弦的两端点的坐标然后代入到抛物线方程后两式相减，可求得直线方程的斜率，最后根据直线的点斜式可求得方程．
解答：
解：此弦不垂直于x轴，故设点（-1，1）为中点的抛物线y2=-8x的弦的两端点为A（x1，y1）B（x2，y2）
得到yi2=-8x1，y22=-8x2
两式相减得到（y1+y2）（y1-y2）=-8（x1-x2）
∵y1+y2=2
∴k=-4
∴直线方程为y+1=-4（x-1），即4x+y+3=0
故选：D．
得到yi2=-8x1，y22=-8x2
两式相减得到（y1+y2）（y1-y2）=-8（x1-x2）
∵y1+y2=2
∴k=-4
∴直线方程为y+1=-4（x-1），即4x+y+3=0
故选：D．
点评：本题主要考查直线和抛物线的综合问题．考查综合运用能力．
练习册系列答案
相关题目
函数y=sin2x的一个单调区间是（ ）
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
D、[
|
已知向量
=（-1，2），
=（x，4），且
∥
，则x的值为（ ）
| a |
| b |
| a |
| b |
| A、8 | B、2 | C、-2 | D、-8 |
已知函数y=-x3+3x-a在[0，2]上有两个零点，则常数a的取值范围为（ ）
| A、0≤a＜2 |
| B、-2≤a≤2 |
| C、-2＜a＜2 |
| D、0≤a≤2 |
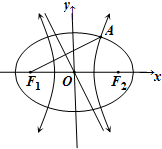如图，F1，F2是椭圆C1：| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 | ||
|
| 1 | ||
|
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
由0，1，2，3这四个数字可以组成没有重复数字且不能被5整除的四位数的个数是（ ）
| A、24个 | B、12个 |
| C、6个 | D、4个 |
抛掷一枚骰子，得到偶数点的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|