题目内容
19. 已知圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,点C是弧AB的中点;
已知圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,点C是弧AB的中点;(1)求三棱锥P-ACO的体积;
(2)求异面直线MC与PO所成的角.
分析 (1)由已知得AB=8,OC=4,OC⊥AB,PO=3,由此能出三棱锥P-ACO的体积.
(2)以O为原点,OC为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出异面直线MC与PO所成的角.
解答 解:(1)∵圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,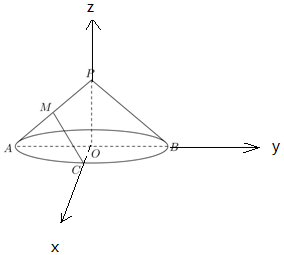
AB是底面圆的直径,点C是弧AB的中点,
∴AB=8,OC=4,OC⊥AB,
∴PO=$\sqrt{P{A}^{2}-A{O}^{2}}$=$\sqrt{25-16}$=3,
∴三棱锥P-ACO的体积VP-ACO=$\frac{1}{3}×{S}_{△AOC}×OP$
=$\frac{1}{3}×\frac{1}{2}×4×4×3$=8.
(2)以O为原点,OC为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,
A(0,-4,0),P(0,0,3),M(0,-2,$\frac{3}{2}$),C(4,0,0),O(0,0,0),
$\overrightarrow{MC}$=(4,2,-$\frac{3}{2}$),$\overrightarrow{PO}$=(0,0,-3),
设异面直线MC与PO所成的角为θ,
cosθ=$\frac{|\overrightarrow{MC}•\overrightarrow{PO}|}{|\overrightarrow{MC}|•|\overrightarrow{PO}|}$=$\frac{\frac{9}{2}}{\sqrt{\frac{89}{4}}•3}$=$\frac{3\sqrt{89}}{89}$,
故异面直线MC与PO所成的角为arccos$\frac{3\sqrt{89}}{89}$.
点评 本题考查柱、锥、台体的体积的求法,考查异面直线所成角的求法,考查空间想象能力与计算能力,是中档题.

 学业测评一课一测系列答案
学业测评一课一测系列答案| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
| A. | 210 | B. | 190 | C. | 220 | D. | 242 |
| A. | $\frac{13}{12}$ | B. | $\frac{12}{5}$ | C. | $\frac{3}{2}$ | D. | 3 |
| A. | [-2,0)∪[3,+∞) | B. | (-∞,-1]∪(0,6] | C. | [-2,-1]∪[3,6] | D. | [-2,0)∪(0,6] |
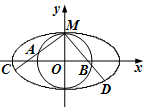 如图,圆O与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)相切于点M(0,1).
如图,圆O与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)相切于点M(0,1).