题目内容
9.已知A(1,2),B(2,11),若直线y=(m-$\frac{6}{m}$)x+1(m≠0)与线段AB相交,则实数m的取值范围是( )| A. | [-2,0)∪[3,+∞) | B. | (-∞,-1]∪(0,6] | C. | [-2,-1]∪[3,6] | D. | [-2,0)∪(0,6] |
分析 由题意知,两点A,B分布在直线的两侧,利用直线两侧的点的坐标代入直线的方程中的左式,得到的结果为异号,得到不等式,解之即得m的取值范围
解答 解:由题意得:
两点A(1,2),B(2,11)分布在直线y=(m-$\frac{6}{m}$)x+1(m≠0)的两侧,
∴(m-$\frac{6}{m}$-2+1)[2(m-$\frac{6}{m}$)-11+1]≤0,
解得:-2≤m≤-1或3≤m≤6,
故选:C.
点评 本小题主要考查二元一次不等式(组)与平面区域、点与直线的位置关系、不等式的解法等基础知识,考查运算求解能力,属于基础题.

练习册系列答案
相关题目
20.执行如图所示的程序框图,则输出S的值为( )
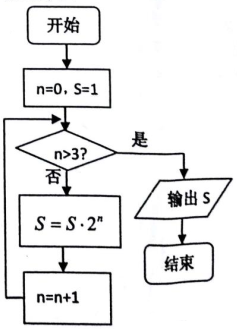

| A. | 16 | B. | 32 | C. | 64 | D. | 1024 |
17.设抛物线x2=4y的焦点为F,过点F作斜率为k(k>0)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,过点P作x轴的垂线与抛物线交于点M,若|MF|=4,则直线l的方程为( )
| A. | $y=2\sqrt{2}x+1$ | B. | $y=\sqrt{3}x+1$ | C. | $y=\sqrt{2}x+1$ | D. | $y=2\sqrt{3}x+2$ |
14.某几何体的三视图如图所示,其俯视图是由一个半圆与其直径组成的图形,则此几何体的体积是( )
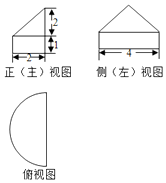

| A. | 3π | B. | $\frac{10π}{3}$ | C. | $\frac{11π}{3}$ | D. | 4π |
1.已知函数f(x)满足条件:?x∈R,f(x)+f(-x)=0且f(x+t)-f(x)<0(其中t为正数),则函数f(x)的解析式可以是( )
| A. | y=xsinx+3 | B. | y=x3 | C. | y=-sinx | D. | y=-3x |
19.已知等差数列{an}的前n项和为Sn,若S10=55,则a3+a8=( )
| A. | 5 | B. | $\frac{11}{2}$ | C. | 10 | D. | 11 |
 已知圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,点C是弧AB的中点;
已知圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,点C是弧AB的中点;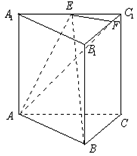 已知直三棱柱ABC-A1B1C1的底面为正三角形,E,F分别是A1C1,B1C1上的点,且满足A1E=EC1,B1F=3FC1.
已知直三棱柱ABC-A1B1C1的底面为正三角形,E,F分别是A1C1,B1C1上的点,且满足A1E=EC1,B1F=3FC1.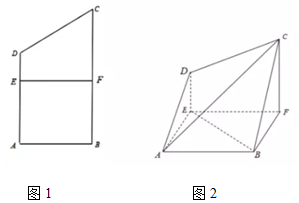 已知四边形ABCD为直角梯形,AD∥BC,AB⊥BC,BC=2AB=4,AD=3,F为BC中点,EF∥AB,EF与AD交于点E,沿EF将四边形EFCD折起,使得平面ABFE⊥平面EFCD,连接AD,BC,AC.
已知四边形ABCD为直角梯形,AD∥BC,AB⊥BC,BC=2AB=4,AD=3,F为BC中点,EF∥AB,EF与AD交于点E,沿EF将四边形EFCD折起,使得平面ABFE⊥平面EFCD,连接AD,BC,AC.