题目内容
4.在二项式(x2-$\frac{1}{x}$)n的展开式中,所有二项式系数的和是32,则展开式中所有整式项的系数和为-4.分析 由题意可得:2n=32,解得n=5.再利用通项公式即可得出.
解答 解:由题意可得:2n=32,解得n=5.
$({x}^{2}-\frac{1}{x})^{5}$的通项公式为:Tr+1=${∁}_{5}^{r}({x}^{2})^{5-r}(-\frac{1}{x})^{r}$=(-1)r${∁}_{5}^{r}$x10-3r.
r=0,1,2,3时,通项为整式项,系数和=1-${∁}_{5}^{1}+{∁}_{5}^{2}-{∁}_{5}^{3}$=-4.
故答案为:-4.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
15.在区间[0,1]上随机选取两个数x和y,则y>2x的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
12.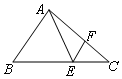 如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )
如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )
 如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )
如图,在△ABC中,E,F分别是边BC,AC上的点,且△ABE是边长为3的正三角形,EF∥AB,EF=1,则sinC等于( )| A. | $\frac{{\sqrt{7}}}{14}$ | B. | $\frac{{\sqrt{7}}}{7}$ | C. | $\frac{{\sqrt{21}}}{14}$ | D. | $\frac{{\sqrt{21}}}{7}$ |
16.在直三棱柱ABC-A1BlC1中,平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确的命题有( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
13.宿州市日前提出,要提升市民的生活质量,改善民生,促进“中国梦”的实线,为此,某记者在街头随机采访了100名市民,根据他们对“中国梦”实线的信心情况进行统计分析,得到如下分布表:
(Ⅰ)以这100名市民信心指数为样本来估计市民的总体信心指数,若要从全市市民中随机任选3人进行信心跟踪,记ξ表示抽到信心级别为“非常有信心或有信心”市民人数,求ξ的分布列及期望;
(Ⅱ)从这100名市民中,任选两人,记他们的信心指数分别为m、n,求|m-n|≥60的概率.
| 信心级别 | 非常有信心 | 有信心 | 不知道 | 没信心 |
| 信心指数(分数) | 90 | 60 | 30 | 6 |
| 人数(名) | 42 | 38 | 14 | 6 |
(Ⅱ)从这100名市民中,任选两人,记他们的信心指数分别为m、n,求|m-n|≥60的概率.
14.某几何体的三视图如图所示,其俯视图是由一个半圆与其直径组成的图形,则此几何体的体积是( )
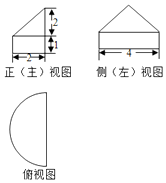

| A. | 3π | B. | $\frac{10π}{3}$ | C. | $\frac{11π}{3}$ | D. | 4π |
 已知圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,点C是弧AB的中点;
已知圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,点C是弧AB的中点;