题目内容
8．在等比数列{an}中，a2•a3是a12和a42的等差中项，则$\frac{{S}_{6}}{{S}_{3}}$=（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 a2•a3是a12和a42的等差中项，可得2a2•a3=a12+a42，2q3=1+q6，解得q．即可得出．
解答 解：∵a2•a3是a12和a42的等差中项，∴2a2•a3=a12+a42，∴2q3=1+q6，解得q3=1，解得q=1．
$\frac{{S}_{6}}{{S}_{3}}$=$\frac{6{a}_{1}}{3{a}_{1}}$=2，
故选：B．
点评 本题考查了等比数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
已知圆锥母线长为5，底面圆半径长为4，点M是母线PA的中点，AB是底面圆的直径，点C是弧AB的中点；
16．在直三棱柱ABC-A1BlC1中，平面α与棱AB，AC，A1C1，A1B1分别交于点E，F，G，H，且直线AA1∥平面α．有下列三个命题：①四边形EFGH是平行四边形；②平面α∥平面BCC1B1；③平面α⊥平面BCFE．其中正确的命题有（ ）
| A． | ①② | B． | ②③ | C． | ①③ | D． | ①②③ |
3．已知角α的终边与单位圆交于点（-$\frac{2\sqrt{5}}{5}$，-$\frac{\sqrt{5}}{5}$），则sin2α的值为（ ）
| A． | $\frac{\sqrt{5}}{5}$ | B． | -$\frac{\sqrt{5}}{5}$ | C． | -$\frac{4}{5}$ | D． | $\frac{4}{5}$ |
13．宿州市日前提出，要提升市民的生活质量，改善民生，促进“中国梦”的实线，为此，某记者在街头随机采访了100名市民，根据他们对“中国梦”实线的信心情况进行统计分析，得到如下分布表：
（Ⅰ）以这100名市民信心指数为样本来估计市民的总体信心指数，若要从全市市民中随机任选3人进行信心跟踪，记ξ表示抽到信心级别为“非常有信心或有信心”市民人数，求ξ的分布列及期望；
（Ⅱ）从这100名市民中，任选两人，记他们的信心指数分别为m、n，求|m-n|≥60的概率．
| 信心级别 | 非常有信心 | 有信心 | 不知道 | 没信心 |
| 信心指数（分数） | 90 | 60 | 30 | 6 |
| 人数（名） | 42 | 38 | 14 | 6 |
（Ⅱ）从这100名市民中，任选两人，记他们的信心指数分别为m、n，求|m-n|≥60的概率．
20．执行如图所示的程序框图，则输出S的值为（ ）
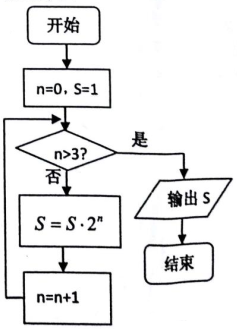
| A． | 16 | B． | 32 | C． | 64 | D． | 1024 |
17．设抛物线x2=4y的焦点为F，过点F作斜率为k（k＞0）的直线l与抛物线相交于A、B两点，且点P恰为AB的中点，过点P作x轴的垂线与抛物线交于点M，若|MF|=4，则直线l的方程为（ ）
| A． | $y=2\sqrt{2}x+1$ | B． | $y=\sqrt{3}x+1$ | C． | $y=\sqrt{2}x+1$ | D． | $y=2\sqrt{3}x+2$ |
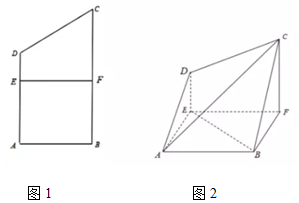已知四边形ABCD为直角梯形，AD∥BC，AB⊥BC，BC=2AB=4，AD=3，F为BC中点，EF∥AB，EF与AD交于点E，沿EF将四边形EFCD折起，使得平面ABFE⊥平面EFCD，连接AD，BC，AC．