题目内容

已知数列{an}中，a1=2，an+an+1=0（n∈N*），则a10的值等于
 
．
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：由题意可得数列{an}为公比为1的等比数列，由通项公式可得．
解答： 解：∵a1=2，an+an+1=0，
∴
an+1
an
=-1，即数列{an}为公比为1的等比数列，
∴a10=a1q9=2×（-1）9=-2
故答案为：-2．
点评：本题考查等比数列的通项公式，得出公比是解决问题的关键，属基础题．
练习册系列答案
相关题目
当a＜0时，函数m（t）=
1
2
at2+t-a的定义域为[
2
，2]，记函数m（t）的最大值为g（a）．
（1）求g（a）的解析式；
（2）试求满足g(a)＞g(
1
a
)的所有实数a的值．
条件p：不等式log2（x-1）＜1的解；条件q：不等式x2-2x-3＜0的解，则p是q的
 
．
已知圆C的圆心是双曲线
y2
12
-
x2
4
=1的上焦点，直线4x-3y-3=0与圆C相交于A，B两点，且|AB|=8，则圆C的方程为
 
．
在△ABC中，sin2C=
3
sinAsinB+sin2B，a=2
3
b，则角C=
 
．
按如下程序框，最后输出i的结果是
 
已知f（x）=sin（x+
π
2
），g（x）=cos（x-
π
2
），则下列结论中正确的序号是
 

（1）函数y=f（x）•g（x）的最小正周期为π．
（2）函数y=f（x）•g（x）的最大值为
1
2
．
（3）函数y=f（x）•g（x）的图象关于点（
π
4
，0）成中心对称      
（4）将函数f（x）的图象向右平移
π
2
个单位后得到函数g（x）的图象．
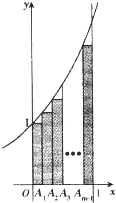如图．A1，A2，…Am-1（m≥2）将区间[0，l]m等分，直线x=0，x=1，y=0和曲线y=ex所围成的区域为Ω1图中m个矩形构成的阴影区域为Ω2．在Ω1中任取一点，则该点取自Ω2的概率等于
 
．
已知集合M={1，z（1+i）}，i为虚数单位，N={3，4}，若M∪N={1，2，3，4}，则复数z在复平面上所对应的点在（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网