题目内容
在△ABC中,sin2C=
sinAsinB+sin2B,a=2
b,则角C= .
| 3 |
| 3 |
考点:正弦定理
专题:三角函数的求值
分析:已知第一个等式利用正弦定理化简,整理后将第二个等式代入用b表示出c,再利用余弦定理表示出cosC,将表示出的a,c代入求出cosC的值,即可确定出C的度数.
解答:
解:在△ABC中,sin2C=
sinAsinB+sin2B,
利用正弦定理化简得:c2=
ab+b2,
将a=2
b代入得:c2=2
b•
b+b2=7b2,即c=
b,
∴cosC=
=
=
,
则C=
.
故答案为:
| 3 |
利用正弦定理化简得:c2=
| 3 |
将a=2
| 3 |
| 3 |
| 3 |
| 7 |
∴cosC=
| a2+b2-c2 |
| 2ab |
| 12b2+b2-7b2 | ||
4
|
| ||
| 2 |
则C=
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:此题考查了正弦、余弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
如果函数y=|cos(
+ax)|的图象关于直线x=π对称,则正实数a的最小值是( )
| π |
| 4 |
A、a=
| ||
B、a=
| ||
C、a=
| ||
| D、a=1 |
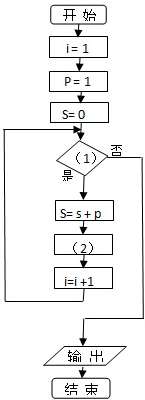 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将右面给出的程序框图补充完整,再将与其功能相当的程序语言补充完整,把答案写在下面空格上.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将右面给出的程序框图补充完整,再将与其功能相当的程序语言补充完整,把答案写在下面空格上.