题目内容
已知f(x)是定义在R上的偶函数,对任意x∈R都有f(x+4)=f(x)+2f(2),且f(-1)=2,则f(2013)等于( )
| A、2 | B、3 | C、4 | D、6 |
考点:函数奇偶性的性质,抽象函数及其应用
专题:计算题,函数的性质及应用
分析:根据偶函数的定义,结合f(x+4)=f(x)+2f(2),令x=-2,求出f(2)=0,从而函数f(x)是周期为4的函数,f(2013)=f(1),再由偶函数的定义得f(1)=f(-1),由条件即得.
解答:
解:∵f(x)是定义在R上的偶函数,
∴f(-2)=f(2),
∵对任意x∈R都有f(x+4)=f(x)+2f(2),
令x=-2,则f(2)=f(-2)+2f(2),
∴f(2)=0,
∴f(x+4)=f(x),
即函数f(x)是最小正周期为4的函数,
∴f(2013)=f(4×503+1)=f(1),
∵f(x)是定义在R上的偶函数,
∴f(-1)=f(1),
又f(-1)=2,
∴f(2013)=2,
故选A.
∴f(-2)=f(2),
∵对任意x∈R都有f(x+4)=f(x)+2f(2),
令x=-2,则f(2)=f(-2)+2f(2),
∴f(2)=0,
∴f(x+4)=f(x),
即函数f(x)是最小正周期为4的函数,
∴f(2013)=f(4×503+1)=f(1),
∵f(x)是定义在R上的偶函数,
∴f(-1)=f(1),
又f(-1)=2,
∴f(2013)=2,
故选A.
点评:本题主要考查函数的周期性及应用,函数的奇偶性的定义和运用,考查解决抽象函数常用的方法:赋值法,正确赋值是解题的关键.

练习册系列答案
相关题目
设双曲线
-
=1(a>0)的渐近线方程为3x±2y=0,则
(
)dx的值为( )
| x2 |
| a2 |
| y2 |
| 9 |
| ∫ | a 1 |
| 1 |
| x |
| A、ln2 | B、0 | C、ln3 | D、1 |
在某次测量中得到的A样本数据如下:42,43,46,52,42,50,若B样本数据恰好是A样本数据每个都减5后所得数据,则A、B两样本的下列数字特征对应相同的是( )
| A、平均数 | B、标准差 |
| C、众数 | D、中位数 |
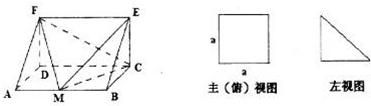
一个多面体的直观图和三视图所示,M是AB的中点,一只蝴蝶在几何体ADF-BCE内自由飞翔,由它飞入几何体F-AMCD内的概率为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
关于x的不等式ax-b>0的解集为(-∞,1),则不等式
>0的解集为( )
| x-2 |
| ax-b |
| A、(-1,2) |
| B、(-∞,1)∪(1,2) |
| C、(1,2) |
| D、(-∞,-1)∪(-1,2) |