Question

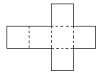如图是一个正方体纸盒的展开图，把1、-1、2、-2、

2

、-

2

分别填入六个正方形，使得按虚线折成正方体后，相对面上的两个数的绝对值相等，求不同填法的种数（　　）

• A、3
• B、6
• C、24
• D、48

Answer 1

考点：排列、组合的实际应用

专题：应用题,排列组合

分析：先把绝对值相等的数分成三组，相对面上的两个数分别填以上三组，对面交换数值，根据分步乘法原理，即可得出结论．

解答： 解：把绝对值相等的数分成三组（1，-1）、（2，-2）、（

2

，-

2

），相对面上的两个数分别填以上三组，不同的填法有

C

1 3

C

1 2

C

1 1

=6种，又相对面交换数值的方法有2×2×2=8种，故共有6×8=48种．
故选：D．

点评：本题考查灵活运用正方体的相对面解答问题，立意新颖，是一道不错的题．