题目内容
北京、张家港2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估.该商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到x元.公司拟投入
(x2-600)万作为技改费用,投入50万元作为固定宣传费用,投入
万元作为浮动宣传费用.试问:当该商品改革后的销售量a至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到x元.公司拟投入
| 1 |
| 6 |
| x |
| 5 |
考点:根据实际问题选择函数类型
专题:综合题,函数的性质及应用
分析:(1)设每件定价为x元,可得提高价格后的销售量,根据销售的总收人不低于原收入,建立不等式,解不等式可得每件最高定价;
(2)依题意,x>25时,不等式ax≥25×8+50+
(x2-600)+
x有解,等价于x>25时,a≥
+
x+
有解,利用基本不等式,我们可以求得结论.
(2)依题意,x>25时,不等式ax≥25×8+50+
| 1 |
| 6 |
| 1 |
| 5 |
| 150 |
| x |
| 1 |
| 6 |
| 1 |
| 5 |
解答:
解:(1)设每件定价为t元,依题意得(8-
×0.2)x≥25×8,
整理得t2-65t+1 000≤0,解得25≤t≤40.
所以要使销售的总收入不低于原收入,每件定价最多为40元.
(2)依题意知当x>25时,不等式ax≥25×8+50+
(x2-600)+
x有解,
等价于x>25时,a≥
+
x+
有解.
由于
+
x≥2
=10,当且仅当
=
,即x=30时等号成立,所以a≥10.2.
当该商品改革后的销售量a至少达到10.2万件时,才可能使改革后的销售收入不低于原收入与总投入之和,此时该商品的每件定价为30元.
| x-25 |
| 1 |
整理得t2-65t+1 000≤0,解得25≤t≤40.
所以要使销售的总收入不低于原收入,每件定价最多为40元.
(2)依题意知当x>25时,不等式ax≥25×8+50+
| 1 |
| 6 |
| 1 |
| 5 |
等价于x>25时,a≥
| 150 |
| x |
| 1 |
| 6 |
| 1 |
| 5 |
由于
| 150 |
| x |
| 1 |
| 6 |
|
| 150 |
| x |
| x |
| 6 |
当该商品改革后的销售量a至少达到10.2万件时,才可能使改革后的销售收入不低于原收入与总投入之和,此时该商品的每件定价为30元.
点评:解决实际问题的关键是读懂题意,建立函数模型,同时应注意变量的取值应使实际问题有意义.

练习册系列答案
相关题目
已知函数①y=3x;②y=lnx;③y=x-1;④y=x
.则下列函数图象(在第一象限部分)从左到右依次与函数序号的对应顺序一致的是( )
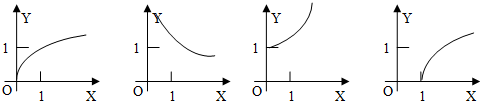
| 1 |
| 2 |
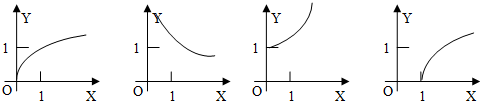
| A、④③①② | B、②③①④ |
| C、④①③② | D、②①③④ |
已知f(3x)=4xlog23,则f(4)的值等于( )
| A、4 | B、8 | C、16 | D、9 |