题目内容
已知f（3x）=4xlog23，则f（4）的值等于（ ）
| A、4 | B、8 | C、16 | D、9 |
考点：对数的运算性质
专题：函数的性质及应用
分析：令3x=t＞0，则x=log3t．f（t）=4log3t•log23．把t=4代入再利用对数的换底公式即可得出．
解答：
解：令3x=t＞0，则x=log3t．
∴f（t）=4log3t•log23．
∴f（4）=4log34•log23
=
•
=8．
故选：B．
∴f（t）=4log3t•log23．
∴f（4）=4log34•log23
=
| 8lg2 |
| lg3 |
| lg3 |
| lg2 |
=8．
故选：B．
点评：本题考查了指数式与对数式的互化、对数的换底公式、换元法，属于基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
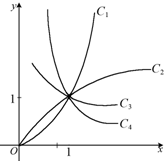如图是幂函数y=xn在第一象限内的图象，已知n取| 1 |
| 2 |
| 1 |
| 2 |
A、2，
| ||||
B、-2，-
| ||||
C、-
| ||||
D、2，
|
已知集合A={x|x＜2
}，a=2，则下列关系正确的是（ ）
| 3 |
| A、a?A | B、{a}∈A |
| C、a∈A | D、a∉A |
下列各图中，表示以x为自变量的函数的图象是（ ）
A、 |
B、 |
C、 |
D、 |