题目内容
11.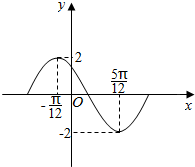 函数y=Asin(ωx+ϕ),(A>0,ω>0,0<ϕ<π)在一个周期内的图象如图所示.
函数y=Asin(ωx+ϕ),(A>0,ω>0,0<ϕ<π)在一个周期内的图象如图所示.(1)求该函数的解析式.
(2)当$x∈[-\frac{π}{2},\frac{π}{6}]$时,求该函数的值域.
分析 (1)由图可知A=2,由周期公式可得ω=2,代入点(-$\frac{π}{12}$,2)可得ϕ=$\frac{2π}{3}$,可得y=2sin(2x+$\frac{2π}{3}$);
(2)由$x∈[-\frac{π}{2},\frac{π}{6}]$,可得2x+$\frac{2π}{3}$∈[$-\frac{π}{3}$,π],结合正弦函数的图象可得.
解答 解:(1)由图可知A=2,T=$\frac{5π}{12}$-(-$\frac{π}{12}$)=$\frac{2π}{ω}$,
解得ω=2,∴y=2sin(2x+ϕ),
代入点(-$\frac{π}{12}$,2)可得2=2sin(-$\frac{π}{6}$+ϕ),
∴sin(-$\frac{π}{6}$+ϕ)=1,-$\frac{π}{6}$+ϕ=$\frac{π}{2}$+2kπ,k∈Z,
∵0<ϕ<π,∴当k=时,ϕ=$\frac{2π}{3}$,
∴函数的解析式为y=2sin(2x+$\frac{2π}{3}$);
(2)∵$x∈[-\frac{π}{2},\frac{π}{6}]$,∴2x+$\frac{2π}{3}$∈[$-\frac{π}{3}$,π],
∴当2x+$\frac{2π}{3}$=$-\frac{π}{3}$即x=$-\frac{π}{2}$时,函数取最小值-$\sqrt{3}$;
当2x+$\frac{2π}{3}$=$\frac{π}{2}$即x=-$\frac{π}{12}$时,函数取最大值2,
故函数的值域为[-$\sqrt{3}$,2].
点评 本题考查三角函数的图象和性质,涉及三角函数的解析式求解和值域,属基础题.

练习册系列答案
相关题目
2.在△ABC中,内角A、B、C所对的边长分别是a、b、c,且边c的长为2,角C为$\frac{π}{3}$,△ABC的面积为$\sqrt{3}$,则a=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
19.设不等式x2-x≤0的解集为M,则M为( )
| A. | [0,1) | B. | (0,1) | C. | [0,1] | D. | (-1,0] |
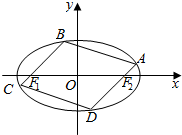 已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),两点F1(-1,0)、F2(1,0)为椭圆C的焦点,点P在椭圆C上,且|PF1|+|PF2|=2|F1F2|.
已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),两点F1(-1,0)、F2(1,0)为椭圆C的焦点,点P在椭圆C上,且|PF1|+|PF2|=2|F1F2|.