题目内容
11.已知数列{an}是公比为2的等比数列,数列{bn}是公差为3且各项均为正整数的等差数列,则数列{a${\;}_{{b}_{n}}$}是( )| A. | 公差为5的等差数列 | B. | 公差为6的等差数列 | ||
| C. | 公比为6的等比数列 | D. | 公比为8的等比数列 |
分析 由数列{an}是公比为2的等比数列,可得${a}_{n}={a}_{1}×{2}^{n-1}$.由数列{bn}是公差为3且各项均为正整数的等差数列,可得bn+1-bn=3,计算$\frac{{a}_{{b}_{n+1}}}{{a}_{{b}_{n}}}$即可判断出结论.
解答 解:由数列{an}是公比为2的等比数列,
可得${a}_{n}={a}_{1}×{2}^{n-1}$.
由数列{bn}是公差为3且各项均为正整数的等差数列,
∴bn+1-bn=3,
则$\frac{{a}_{{b}_{n+1}}}{{a}_{{b}_{n}}}$=$\frac{{a}_{1}{2}^{{b}_{n+1}-1}}{{a}_{1}{2}^{{b}_{n}-1}}$=${2}^{{b}_{n+1}-{b}_{n}}$=23=8.
∴数列{a${\;}_{{b}_{n}}$}是公比为8的等比数列.
故选:D.
点评 本题考查了等差数列与等比数列的定义及其通项公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知sinθ-2cosθ=0,则cos2θ-sin2θ=( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
19.“x<4”是“|x-2|<1”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
6.已知命题:p?x∈(0,$\frac{π}{2}$),sinx+cosx>1恒成立,命题q:?x∈(0,$\frac{π}{2}$),使2x>3x,则下列结论中正确的是( )
| A. | 命题“p∧q”是真命题 | B. | 命题“p∧(¬q)”是真命题 | ||
| C. | 命题“(¬p)∧q”为真命题 | D. | 命题“(¬p)∧(¬q)”是真命题 |
16.已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-1,m),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则m=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
3.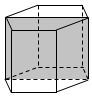 如图,已知正六棱柱的最大对角面的面积为1m2,互相平行的两个侧面的距离为1m,则这个六棱柱的体积为( )
如图,已知正六棱柱的最大对角面的面积为1m2,互相平行的两个侧面的距离为1m,则这个六棱柱的体积为( )
 如图,已知正六棱柱的最大对角面的面积为1m2,互相平行的两个侧面的距离为1m,则这个六棱柱的体积为( )
如图,已知正六棱柱的最大对角面的面积为1m2,互相平行的两个侧面的距离为1m,则这个六棱柱的体积为( )| A. | $\frac{{3\sqrt{3}}}{4}$m3 | B. | $\frac{3}{4}$m3 | C. | 1m3 | D. | $\frac{1}{2}$m3 |
20.若函数f(x)=(k2+1)lnx-x2在区间(1,+∞)上是减函数,则实数k的取值范围是( )
| A. | [-1,1] | B. | [-$\sqrt{2}$,$\sqrt{2}$] | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-$\sqrt{2}$]∪[$\sqrt{2}$,+∞) |
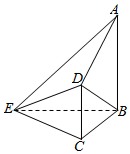 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=$\frac{2π}{3}$.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=$\frac{2π}{3}$.