题目内容
6.已知命题:p?x∈(0,$\frac{π}{2}$),sinx+cosx>1恒成立,命题q:?x∈(0,$\frac{π}{2}$),使2x>3x,则下列结论中正确的是( )| A. | 命题“p∧q”是真命题 | B. | 命题“p∧(¬q)”是真命题 | ||
| C. | 命题“(¬p)∧q”为真命题 | D. | 命题“(¬p)∧(¬q)”是真命题 |
分析 分别判断出命题p,q的真假,从而得到答案.
解答 解:命题:p:?x∈(0,$\frac{π}{2}$),sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)∈(1,$\sqrt{2}$];p真,
命题q::x∈(0,$\frac{π}{2}$),∵${(\frac{3}{2})}^{x}$>1,∴3x>2x,故q是假命题,
故p∧q假,A错误,p∧(¬q)真,B正确,
(¬p)∧q假,C错误,(¬p)∧(¬q)假,D错误;
故选:B.
点评 本题考查了复合命题的判断,考查三角函数的性质,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.命题“?x∈R,x2≠x”的否定是( )
| A. | ?x∉R,x2≠x | B. | ?x∈R,x2=x | C. | ?x0∈R,x${\;}_{0}^{2}$≠x0 | D. | ?x0∈R,x${\;}_{0}^{2}$=x0 |
11.已知数列{an}是公比为2的等比数列,数列{bn}是公差为3且各项均为正整数的等差数列,则数列{a${\;}_{{b}_{n}}$}是( )
| A. | 公差为5的等差数列 | B. | 公差为6的等差数列 | ||
| C. | 公比为6的等比数列 | D. | 公比为8的等比数列 |
15.已知复数Z的共轭复数$\overline{Z}$=$\frac{1-i}{1+2i}$,则复数Z的虚部是( )
| A. | $\frac{3}{5}$ | B. | $\frac{3}{5}$i | C. | -$\frac{3}{5}$ | D. | -$\frac{3}{5}$i |
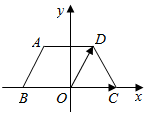 如图,在直角坐标平面内,等腰梯形ABCD的下底BC在x轴上,BC的中点是坐标原点0,已知AD=AB=DC=1,BC=2.
如图,在直角坐标平面内,等腰梯形ABCD的下底BC在x轴上,BC的中点是坐标原点0,已知AD=AB=DC=1,BC=2.