题目内容
14.已知sinθ-2cosθ=0,则cos2θ-sin2θ=( )| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
分析 利用同角三角函数关系式及二倍角公式求解.
解答 解:∵sinθ-2cosθ=0,∴sinθ=2cosθ,
∴cos2θ+sin2θ=5cos2θ=1,
∴cos2θ=$\frac{1}{5}$,
又(sinθ-2cosθ)2=sin2θ-4sinθcosθ+4cos2θ=0;
∴sin2θ=2sinθcosθ=$\frac{4}{5}$;
∴cos2θ-sin2θ=$\frac{1}{5}$-$\frac{4}{5}$=-$\frac{3}{5}$;
故选:B.
点评 本题考查三角函数值的求法,是基础题,解题时要认真审题,注意同角三角函数关系式、二倍角公式的合理运用.

练习册系列答案
相关题目
6.下列说法正确的是( )
| A. | y=sinx在第三象限内是增函数 | B. | 函数y=sinx(x∈R)的值域是(-1,1) | ||
| C. | y=cosx在x=2kπ(k∈Z)时取值最大 | D. | y=tanx在整个定义域内都是增函数 |
3.设正数x,y满足-1<x-y<2,则z=2x-2y的取值范围为( )
| A. | (-∞,4) | B. | (0,4) | C. | ($\frac{1}{4}$,4) | D. | (4,+∞) |
11.已知数列{an}是公比为2的等比数列,数列{bn}是公差为3且各项均为正整数的等差数列,则数列{a${\;}_{{b}_{n}}$}是( )
| A. | 公差为5的等差数列 | B. | 公差为6的等差数列 | ||
| C. | 公比为6的等比数列 | D. | 公比为8的等比数列 |
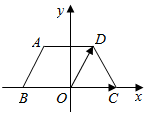 如图,在直角坐标平面内,等腰梯形ABCD的下底BC在x轴上,BC的中点是坐标原点0,已知AD=AB=DC=1,BC=2.
如图,在直角坐标平面内,等腰梯形ABCD的下底BC在x轴上,BC的中点是坐标原点0,已知AD=AB=DC=1,BC=2.