题目内容
若函数f(x2)=x4+x2,则函数f(x)的解析式为 .
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:本题可以利用换元法求出函数的解析式,要注意函数自变量x的取值范围.
解答:
解:∵函数f(x2)=x4+x2,
∴令t=x2,
则x4=t2,
∴f(t)=t2+t,(t≥0),
即f(x)=x2+x,(x≥0).
故答案为:f(x)=x2+x,(x≥0).
∴令t=x2,
则x4=t2,
∴f(t)=t2+t,(t≥0),
即f(x)=x2+x,(x≥0).
故答案为:f(x)=x2+x,(x≥0).
点评:本题考查了函数解析式的求法,本题难度不大,属于基础题.

练习册系列答案
相关题目
下列各式错误的是( )
| A、tan138°<tan143° | ||||
B、sin(-
| ||||
| C、lg1.6>lg1.4 | ||||
| D、0.75-0.1<0.750.1 |
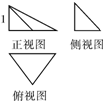 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积是( )| A、36π | ||
| B、9π | ||
C、
| ||
D、
|
已知某几何体的三视图如上图所示(单位:cm),则该几何体的表面积是( )
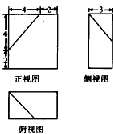

A、(124+2
| ||
| B、92cm2 | ||
| C、124cm2 | ||
| D、84cm2 |
已知定义在R上的单调函数f(x)满足:存在实数x0,使得对于任意实数x1,x2,总有f(x0x1+x0x2)=f(x0)+f(x1)+f(x2)恒成立.求:
(1)f(1)+f(0);
(2)x0的值.
(1)f(1)+f(0);
(2)x0的值.
在△ABC中,角A,B,C所对的边分别为a,b,c,S表示△ABC的面积,若acosB+bcosA=csinC,S=
(b2+c2-a2),则∠B=( )
| 1 |
| 4 |
| A、90° | B、60° |
| C、45° | D、30° |
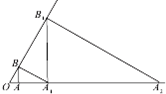 如图,在△OAB中,OA⊥AB,OB=1,OA=
如图,在△OAB中,OA⊥AB,OB=1,OA=