题目内容
在复平面内,复数
(i是虚数单位)所对应的点位于( )
| 2 |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:复数代数形式的乘除运算,复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:利用复数代数形式的乘除运算法则和复数的几何意义求解.
解答:
解:
=
=
=1-i,
∴在复平面内,
复数
(i是虚数单位)所对应的点(1,-1)位于第四象限.
故选:D.
| 2 |
| 1+i |
| 2(1-i) |
| (1+i)(1-i) |
=
| 2-2i |
| 2 |
=1-i,
∴在复平面内,
复数
| 2 |
| 1+i |
故选:D.
点评:本题考查复数所对应的点在第几象限的求法,解题时要认真审题,是基础题.

练习册系列答案
相关题目
一半径为r的圆内切于半径为3r、圆心角为α(0<α<
)的扇形,则该圆的面积与该扇形的面积之比为( )
| π |
| 2 |
| A、3:4 | B、2:3 |
| C、1:2 | D、1:3 |
下列关系式中,正确的是( )
| A、(sinx)′=cosx |
| B、(sinx)′=-cosx |
| C、(cosx)′=cosx |
| D、(cosx)′=sinsx |
函数f(α)=tsinα+cosα的最大值为g(t),则g(t)的最小值为( )
| A、1 | ||
| B、0 | ||
| C、|t|+1 | ||
D、
|
在某县临时客车停靠站,每天均有上、中、下等级的客车各一辆开往城区.某天李先生准备从该站点前往城区办事,但他不知道客车的车况,也不知道发车顺序,为了尽可能乘到上等车,他采取如下策略:先放过第一辆,如果第二辆比第一辆好,则上第二辆,否则上第三辆,那么李先生乘到上等车的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
从一个三棱柱的6个顶点中任取4个做为顶点,能构成三棱锥的个数设为m;过三棱柱任意两个顶点的直线(15条)中,其中能构成异面直线有n对,则m,n的取值分别为( )
| A、15,45 |
| B、10,30 |
| C、12,36 |
| D、12,48 |
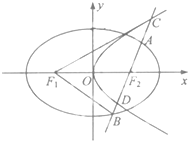 设椭圆C1:
设椭圆C1: