题目内容
15.某民调机构为了了解民众是否支持英国脱离欧盟,随机抽调了100名民众,他们的年龄的频数及支持英国脱离欧盟的人数分布如下表:| 年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
| 频数 | 35 | 20 | 25 | 20 |
| 支持脱欧的人数 | 10 | 10 | 15 | 15 |
| 年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
| 支持“脱欧”人数 | |||
| 不支持“脱欧”人数 | |||
| 合计 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
分析 (Ⅰ)根据统计数据,可得2×2列联表,根据列联表中的数据,计算K2的值,即可得到结论;
(Ⅱ)利用列举法确定基本事件的个数,即可得出这2人至少有1人年龄在18-24岁的概率.
解答 解:(Ⅰ)
| 年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
| 支持“脱欧”人数 | 20 | 30 | 50 |
| 不支持“脱欧”人数 | 35 | 15 | 50 |
| 合计 | 55 | 45 | 100 |
所以有99%的把握认为以50岁为分界点对是否支持脱离欧盟的态度有差异.
(Ⅱ)18-24岁2人,25-49岁2人,50-64岁3人.
记18-24岁的两人为A,B;25-49岁的两人为C,D;50-64岁的三人为E,F,G,
则AB,AC,AD,AE,AF,AG,BC,BD,BE,BF,BG,CD,CE,CF,CG,DE,DF,DG,EF,EG,FG共21种,
其中含有A或B的有11种.
故$P=\frac{11}{21}$.
点评 本题考查独立性检验,考查概率的计算,考查学生的阅读与计算能力,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
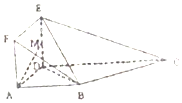 如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.
如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.