题目内容
2.已知全集U=R,集合A={x|2<x<9},B={x|-2≤x≤5}.(1)求A∩B;B∪(∁UA);
(2)已知集合C={x|a≤x≤2-a},若C∪(∁UB)=R,求实数a的取值范围.
分析 (1)根据交集与并集、补集的定义进行计算即可;
(2)根据补集与并集的定义,得出关于a的不等式组,求出解集即可.
解答 解:(1)全集U=R,集合A={x|2<x<9},B={x|-2≤x≤5};
∴A∩B={x|2<x≤5};
∁UA={x|x≤2或x≥9},
∴B∪(CUA)={x|x≤5,或x≥9};
(2)∵∁UB={x|x<-2或x>5},
又集合C={x|a≤x≤2-a},且C∪(∁UB)=R,
∴$\left\{\begin{array}{l}{a≤2-a}\\{a≤-2}\\{2-a≥5}\end{array}\right.$,
解得a≤-3,
∴实数a的取值范围是a≤-3.
点评 本题考查了集合的定义与运算问题,是基础题目.

练习册系列答案
相关题目
12.衡州市临枣中学高二某小组随机调查芙蓉社区160个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,得到下面的数据表:
下面临界值表:
${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}},n=a+b+c+d$
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分别列和期望;
(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 100 | 120 |
| 女 | 20 | 20 | 40 |
| 合计 | 40 | 120 | 160 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分别列和期望;
(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
13.设集合$A=\left\{{x\left|{\frac{2x+1}{x-2}≤0}\right.}\right\}$,B={x|x<1},则A∪B=( )
| A. | $[{-\frac{1}{2},1})$ | B. | (-1,1)∪(1,2) | C. | (-∞,2) | D. | $[{-\frac{1}{2},2})$ |
17.执行如图所示的程序框图,若输入m=4,t=3,则输出y=( )


| A. | 183 | B. | 62 | C. | 61 | D. | 184 |
14.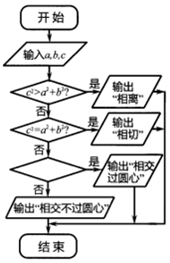 如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )
如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )
 如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )
如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )| A. | c=0? | B. | b=0? | C. | a=0? | D. | ab=0? |
11.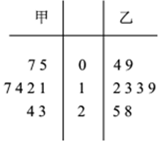 如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )
如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )
 如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )
如图是甲、乙两个商场统计同一时间段各自每天的销售额(单位:万元)的茎叶图,假设销售额的中位数为m,平均值为$\overline{x}$,则下列正确的是( )| A. | m甲=m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | B. | m甲=m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | ||
| C. | m甲>m乙,$\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | D. | m甲<m乙,$\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ |
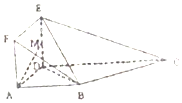 如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.
如图,在多面体ABCDEF中,平面ADEF与平面ABCD垂直,ADEF是正方形,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=$\frac{1}{2}$CD=1,M为线段ED的中点.