题目内容
10．已知：①tan（-3）；②sin4；③cos5；④tan8；其中值为正数的是（ ）| A． | ①② | B． | ①③ | C． | ②③ | D． | ②④ |
分析 根据1rad=$（\frac{180}{π}）^{°}$≈57.30°，利用诱导公式即可得出．
解答 解：1rad=$（\frac{180}{π}）^{°}$≈57.30°．
①tan（-3）=-tan3＞0；
②sin4=-sin（2π-4）＜0；
③cos5=cos（2π-5）＞0；
④tan8=-tan（3π-8）＜0．
综上可得：只有①③为正数，
故选：B．
点评 本题考查了诱导公式、三角函数求值、弧度与角度的互化，考查了推理能力与计算能力，属于中档题．
练习册系列答案
百年学典课时学练测系列答案
相关题目
1．函数f（x）=x+$\frac{{a}^{2}}{x}$（a＞0）的减区间为（ ）
| A． | （-a，a） | B． | （-a，0），（0，a） | C． | （-a，0）∪（0，a） | D． | 以上皆非 |
5．下列各等式中成立的是（ ）
①lg$\frac{1}{100}$=-2；②log3$\sqrt{{3}^{3}}$=$\frac{3}{2}$；③ln$\frac{1}{e}$=-1；④ln0=1；⑤logaa=1（a∈R）
①lg$\frac{1}{100}$=-2；②log3$\sqrt{{3}^{3}}$=$\frac{3}{2}$；③ln$\frac{1}{e}$=-1；④ln0=1；⑤logaa=1（a∈R）
| A． | ①②③ | B． | ①③④ | C． | ①②③④ | D． | ①②③④⑤ |
15．化简sin2β+cos4β+sin2βcos2β的结果是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | $\frac{3}{2}$ |
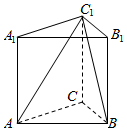如图，三棱柱的侧棱长为2，底面是边长为2的正三角形，AA1⊥面A1B1C1，正视图是边长为2正方形．