题目内容
2.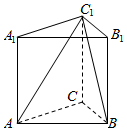 如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正视图是边长为2正方形.
如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正视图是边长为2正方形.(Ⅰ)画出该三棱柱的侧视图,并求其侧视图的面积;
(Ⅱ)求点B1到面ABC1的距离.
分析 (Ⅰ)分析得等边三角形的高,那么侧视图的面积=等边三角形的高×侧棱长,把相关数值代入即可求解;
(Ⅱ)利用等体积转化,求点B1到面ABC1的距离.
解答 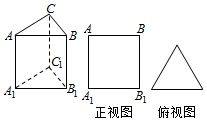 解:(Ⅰ)三棱柱的侧视图如图所示
解:(Ⅰ)三棱柱的侧视图如图所示
∵三棱柱的底面为等边三角形,边长为2,
作出等边三角形的高后,组成直角三角形,底边的一半为1,
∴等边三角形的高为$\sqrt{3}$,
由题意知侧视图是一个高为2,宽为$\sqrt{3}$的矩形,
∴侧视图的面积为2$\sqrt{3}$;
(Ⅱ)设点B1到面ABC1的距离为h,则
△ABC1中,AB=2,AC1=BC1=2$\sqrt{2}$,面积为$\frac{1}{2}×2×\sqrt{8-1}$=$\sqrt{7}$,
由等体积可得$\frac{1}{3}×\sqrt{7}×h=\frac{1}{3}×\frac{1}{2}×2×2×\sqrt{3}$,∴h=$\frac{2\sqrt{21}}{7}$,
∴点B1到面ABC1的距离为$\frac{2\sqrt{21}}{7}$.
点评 本题是中档题,考查点B1到面ABC1的距离,考查几何体的三视图的识别能力,作图能力,三视图的投影规则是主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
10.已知:①tan(-3);②sin4;③cos5;④tan8;其中值为正数的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
14.三角函数y=sin($\frac{π}{6}$-2x)+cos2x的振幅和最小正周期分别为( )
| A. | $\sqrt{3}$,$\frac{π}{2}$ | B. | $\sqrt{3}$,π | C. | $\sqrt{2}$,$\frac{π}{2}$ | D. | $\sqrt{2}$,π |
12.以下表示x轴的参数方程是( )
| A. | $\left\{\begin{array}{l}{x={t}^{2}+1}\\{y=0}\end{array}\right.$(t为参数) | B. | $\left\{\begin{array}{l}{x=0}\\{y=3t+1}\end{array}\right.$(t为参数) | ||
| C. | $\left\{\begin{array}{l}{x=1+sinθ}\\{y=0}\end{array}\right.$(θ为参数) | D. | $\left\{\begin{array}{l}{x=4t+1}\\{y=0}\end{array}\right.$(t为参数) |
 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=$\frac{π}{3}$.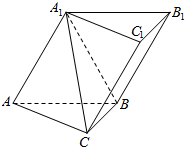 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,AB⊥BC,CB=3,AB=4,∠A1AB=60°.
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,AB⊥BC,CB=3,AB=4,∠A1AB=60°.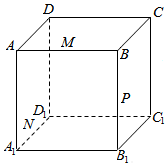 如图所示,正方体ABCD-A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1,BB1的中点.
如图所示,正方体ABCD-A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1,BB1的中点.