题目内容
20.已知二次函数y=αx2+bx+c的图象如图所示.则不等式ax2+bx+c<0的解集为(-1,3).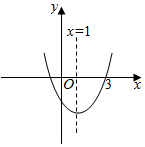
分析 由图象可得a>0,对称轴为x=1,与x轴的交点为(-1,0),(3,0),结合图象即可得到解集.
解答 解:由图象可得,a>0,对称轴为x=1,
可得-1,3是方程αx2+bx+c=0的两根,
则不等式ax2+bx+c<0的解集为(-1,3).
故答案为:(-1,3).
点评 本题考查二次不等式的解法,考查数形结合的思想方法,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列选项中,说法正确的是( )
| A. | 已知命题p和q,若“p∨q”为假命题,则命题p和q中必一真一假 | |
| B. | 命题“?c∈R,方程2x2+y2=c表示椭圆”的否定是“?c∈R,方程2x2+y2=c不表示椭圆” | |
| C. | 命题“若k<9,则方程“$\frac{x^2}{25-k}$+$\frac{y^2}{k-9}$=1表示双曲线”是假命题 | |
| D. | 命题“在△ABC中,若sinA<$\frac{1}{2}$,则A<$\frac{π}{6}$”的逆否命题为真命题 |
5.已知f(x)=2sin(2x+θ+$\frac{π}{3}$)
(1)若0≤θ≤π,求θ,使函数f(x)是偶函数;
(2)在(1)成立的条件下,求满足f(x)=1,其中x∈[-π,π]的x的取值集合.
(1)若0≤θ≤π,求θ,使函数f(x)是偶函数;
(2)在(1)成立的条件下,求满足f(x)=1,其中x∈[-π,π]的x的取值集合.
10.已知:①tan(-3);②sin4;③cos5;④tan8;其中值为正数的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |