题目内容
2．假如现在时间是下午四点整，请问手表上时针与分针所成的角是多少度（写出其中个即可），到当天晚上六点半时，时针和分针各转了多少度？分析 钟面一周为360°，共分12大格，每格为360÷12=30°，下午4时整，分针与时针相差4个整大格，所以钟面上时针与分针形成的夹角是：30°×4=120°；根据时钟上的时针匀速旋转一分钟的度数是0.5°，即可得出从下午4点到下午6点半时针旋转的度数；先求出时钟上的分针匀速旋转一分钟的度数为6°，再求从下午4点到下午6点半分针旋转的度数，从而得解．
解答 解：下午4时整，分针与时针相差4个整大格，
所以钟面上时针与分针形成的夹角是：30°×4=120°；
从下午4点到下午6点半有150分钟，
因为根据时钟上的时针匀速旋转一分钟的度数是0.5°，
那么从下午4点到下午6点半，时针旋转了150×0.5°=75°；
因为时钟上的分针匀速旋转一分钟的度数为6°，
那么从下午4点到下午6点半，分针旋转了150×5°=750°．
点评 本题要在了解钟面结构的基础上进行解答，主要考查了钟面上的路程问题和钟表指针转过的角度计算，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
10．已知：①tan（-3）；②sin4；③cos5；④tan8；其中值为正数的是（ ）
| A． | ①② | B． | ①③ | C． | ②③ | D． | ②④ |
14．三角函数y=sin（$\frac{π}{6}$-2x）+cos2x的振幅和最小正周期分别为（ ）
| A． | $\sqrt{3}$，$\frac{π}{2}$ | B． | $\sqrt{3}$，π | C． | $\sqrt{2}$，$\frac{π}{2}$ | D． | $\sqrt{2}$，π |
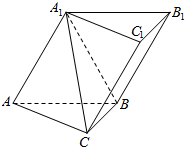如图，在三棱柱ABC-A1B1C1中，四边形A1ABB1是菱形，四边形BCC1B1是矩形，AB⊥BC，CB=3，AB=4，∠A1AB=60°．