题目内容
3.直线l⊥平面α,垂足是点P,正四面体OABC的棱长为2,点O在平面α上运动,点A在直线l上运动,则点P到直线BC的距离的最大值为$\sqrt{2}+1$.分析 P到BC的距离为四面体上以AO为直径的球面上的点到BC的距离,最大距离为BC到球心的距离(即AO与BC的公垂线)+半径.
解答 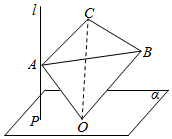 解:由题意,直线AO与动点P的空间关系:
解:由题意,直线AO与动点P的空间关系:
点P是以AO为直径的球面上的点,
∴P到BC的距离为四面体上以AO为直径的球面上的点到BC的距离,
最大距离为BC到球心的距离(即AO与BC的公垂线)+半径,
∵正四面体OABC的棱长为2,∴AO与BC的公垂线长为:$\sqrt{(4-1)-1}$=$\sqrt{2}$,
以AO为直径的球的半径r=1,
点P到直线BC的距离的最大值为$\sqrt{2}+1$.
故答案为:$\sqrt{2}+1$.
点评 本题考查点到直线的最大值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
10.已知:①tan(-3);②sin4;③cos5;④tan8;其中值为正数的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
12.以下表示x轴的参数方程是( )
| A. | $\left\{\begin{array}{l}{x={t}^{2}+1}\\{y=0}\end{array}\right.$(t为参数) | B. | $\left\{\begin{array}{l}{x=0}\\{y=3t+1}\end{array}\right.$(t为参数) | ||
| C. | $\left\{\begin{array}{l}{x=1+sinθ}\\{y=0}\end{array}\right.$(θ为参数) | D. | $\left\{\begin{array}{l}{x=4t+1}\\{y=0}\end{array}\right.$(t为参数) |
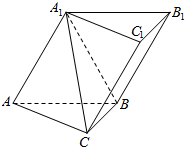 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,AB⊥BC,CB=3,AB=4,∠A1AB=60°.
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,AB⊥BC,CB=3,AB=4,∠A1AB=60°.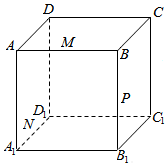 如图所示,正方体ABCD-A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1,BB1的中点.
如图所示,正方体ABCD-A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1,BB1的中点.