题目内容
18.函数f(x)=loga(1-$\frac{a}{x}$)在($\frac{1}{2}$,2)上是减函数,求实数a的范围.分析 先将函数f(x)=loga(2-ax)转化为y=logat,t=1-$\frac{a}{x}$,两个基本函数,再利用复合函数的单调性求解.
解答 解:令y=logat,t=1-$\frac{a}{x}$,
(1)若0<a<1,则y=logat是减函数,
由题设知t=1-$\frac{a}{x}$为增函数,
则:t′=$\frac{a}{{x}^{2}}$>0,
需a>0,且1-$\frac{a}{x}$>0,x∈($\frac{1}{2}$,2),
解得:0<a<$\frac{1}{2}$,
(2)若a>1,则函数y=logat是增函数,则t=1-$\frac{a}{x}$为减函数,
则:t′=$\frac{a}{{x}^{2}}$<0,
需a<0,无解.
综上可得实数a 的取值范围是(0,$\frac{1}{2}$).
点评 本题主要考查了复合函数的单调性,考查了导数的应用,对数的图象和性质,关键是分解为两个基本函数,利用同增异减的结论研究其单调性,再求参数的范围,属于中档题.

练习册系列答案
相关题目
10.已知:①tan(-3);②sin4;③cos5;④tan8;其中值为正数的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
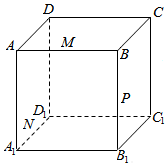 如图所示,正方体ABCD-A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1,BB1的中点.
如图所示,正方体ABCD-A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1,BB1的中点.