题目内容
已知正实数x,y,z满足x2+y2+z2=4,则
xy+yz的最大值为 .
| 2 |
考点:二维形式的柯西不等式
专题:计算题,不等式的解法及应用
分析:由于1=x2+y2+z2=(x2+
y2)+(
y2+z2),利用基本不等式,即可求出
xy+yz的最大值.
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
解答:
解:由于1=x2+y2+z2=(x2+
y2)+(
y2+z2)≥2
xy+2
yz=
(
xy+yz)
∴
xy+yz≤
,
∴
xy+yz的最大值为
,
故答案为:
.
| 2 |
| 3 |
| 1 |
| 3 |
|
|
2
| ||
| 3 |
| 2 |
∴
| 2 |
| ||
| 2 |
∴
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查求
xy+yz的最大值,考查基本不等式的运用,正确运用基本不等式是关键.
| 2 |

练习册系列答案
相关题目
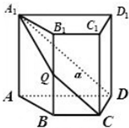 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则| B1Q |
| QB |
| A、1 | ||
| B、2 | ||
| C、3 | ||
D、与
|
已知F是双曲线
-
=1(a>0,b>0)的焦点,A是相应的顶点,P是y轴上的点,满足∠FPA=α,则双曲线的离心率的最小值为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数y=f(x)在R上有定义,对于任一给定的正数p,定义函数fp(x)=
,则称函数fp(x)为f(x)的“p界函数”,若给定函数f(x)=x2-2x-2,p=1,则下列结论成立的是( )
|
| A、fp[f(0)]=f[fp(0)] |
| B、fp[f(1)]=f[fp(1)] |
| C、fp[f(2)]=fp[fp(2)] |
| D、f[f(-2)]=fp[fp(-2)] |
 一几何体三视图为如图所示的三个直角三角形,且该几何体所有棱中最长棱为1,且满足a+
一几何体三视图为如图所示的三个直角三角形,且该几何体所有棱中最长棱为1,且满足a+