题目内容
已知F是双曲线
-
=1(a>0,b>0)的焦点,A是相应的顶点,P是y轴上的点,满足∠FPA=α,则双曲线的离心率的最小值为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:计算题,不等式的解法及应用,圆锥曲线的定义、性质与方程
分析:设F为双曲线的右焦点,且为(c,0),右顶点A(a,0),设|OP|=h,则tanα=tan(∠FPO-∠APO),运用两角差的正切公式,结合基本不等式,得到e的不等式解得e即可,再由同角公式化简即可得到.
解答:
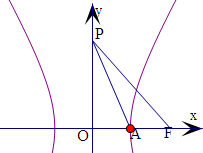 解:设F为双曲线的右焦点,且为(c,0),右顶点A(a,0),
解:设F为双曲线的右焦点,且为(c,0),右顶点A(a,0),
设|OP|=h,
则tanα=tan(∠FPO-∠APO)=
=
=
,
由于h+
≥2
,当且仅当h=
时,取等号.
即有tanα≤
,
即2tanα≤
-
,
即有2tanα≤
-
,即e-2
tanα-1≥0,
即
≥tanα+
,
即有e≥(
)2=
=
=
.
当且仅当h=
时,e的最小值为
.
故选:C.
 解:设F为双曲线的右焦点,且为(c,0),右顶点A(a,0),
解:设F为双曲线的右焦点,且为(c,0),右顶点A(a,0),设|OP|=h,
则tanα=tan(∠FPO-∠APO)=
| tan∠FPO-tan∠APO |
| 1+tan∠FPOtan∠APO |
=
| ||||
1+
|
| c-a | ||
h+
|
由于h+
| ac |
| h |
| ac |
| ac |
即有tanα≤
| c-a | ||
2
|
即2tanα≤
|
|
即有2tanα≤
| e |
|
| e |
即
| e |
| 1+tan2α |
即有e≥(
| 1+sinα |
| cosα |
| (1+sinα)2 |
| cos2α |
| (1+sinα)2 |
| 1-sin2α |
=
| 1+sinα |
| 1-sinα |
当且仅当h=
| ac |
| 1+sinα |
| 1-sinα |
故选:C.
点评:本题考查双曲线的方程和性质,考查基本不等式的运用,运用两角差的正切公式是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
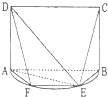 如图,E是以AB为直径的半圆O上异于点A,B的点,边长为4的正方形ABCD所在的平面垂直于该半圆所在的平面.
如图,E是以AB为直径的半圆O上异于点A,B的点,边长为4的正方形ABCD所在的平面垂直于该半圆所在的平面.