题目内容

设函数y=f（x）在R上有定义，对于任一给定的正数p，定义函数fp（x）=
f(x)，f(x)≤p
p，f(x)＞p
，则称函数fp（x）为f（x）的“p界函数”，若给定函数f（x）=x2-2x-2，p=1，则下列结论成立的是（　　）
A、fp[f（0）]=f[fp（0）]
B、fp[f（1）]=f[fp（1）]
C、fp[f（2）]=fp[fp（2）]
D、f[f（-2）]=fp[fp（-2）]
考点：二次函数的性质
专题：函数的性质及应用
分析：根据p界函数的定义求出f1（x）=
x2-2x-2-1≤x≤3
1x＞3，或x＜-1
，从而根据已知函数解析式求函数值，进行验证各选项的正误即可．
解答： 解：根据题意f1(x)=
x2-2x-2-1≤x≤3
1x＞3，或x＜-1
；
∴f（0）=-2，f1（0）=-2，f1[f（0）]=f1（-2）=1，f[f1（0）]=f（-2）=6，∴A错误；
f（1）=-3，f1（1）=-3，f1[f（1）]=f1（-3）=1，f[f1（1）]=f（-3）=13，∴B错误；
f（2）=-2，f1（2）=-2，f1[f（1）]=f1（-2）=1，f1[f1（2）]=f1（-2）=1，∴C正确；
f（-2）=6，f1（-2）=1，f[f（-2）]=f（6）=22，f1[f1（-2）]=f1（1）=-3，∴D错误．
故选C．
点评：考查对p界函数的理解与运用，已知函数解析式能够求出函数值．
练习册系列答案
相关题目
设平面向量
a
=（
3
2
，-
1
2
），
b
=（
1
2
，
3
2
）若存在不同时为零的两个实数s、t及实数k，使
x
=
a
+（t2-k）
b
，
y
=-s
a
+t
b
，且
x
⊥
y

（1）求函数关系式S=f（t）；
（2）若函数S=f（t）在[1，+∞]上是单调函数，求k的取值范围．
已知函数f（x）=lnx-
1
x
，g（x）=ax+b．
（1）若函数h（x）=f（x）-g（x）在（0，+∞）上单调递增，求实数a的取值范围；
（2）若直线g（x）=ax+b是函数f（x）=lnx-
1
x
图象的切线，求a+b的最小值；
（3）当b=0时，若f（x）与g（x）的图象有两个交点A（x1，y1），B（x2，y2），求证：x1x2＞2e2．
（取e为2.8，取ln2为0.7，取
2
为1.4）
已知正实数x，y，z满足x2+y2+z2=4，则
2
xy+yz的最大值为
 
．
四个数排成一串，已知前三个数成等差数列，后三个数成等比数列，且第二个数与第三个数之和为8，第一个数与第四个数之和为16，求这四个数．
已知f（x）=xlnx-
1
2
mx2-x，x∈R．
（Ⅰ）当m=-2时，求函数f（x）的所有零点；
（Ⅱ）若f（x）有两个极值点x1，x2，且x1＜x2，求证：x1x2＞e2（e为自然对数的底数）．
在直角坐标系中，A（-2，0），B（2，0）是两个定点，C（0，p）．D（0，q）是两个动点，且pq=3．
（Ⅰ）求直线AC与BD交点的轨迹M的方程；
（Ⅱ）已知点P（1，t）是轨迹M上位于x轴上方的定点，E，F是轨迹M上的两个动点，直线PE与直线PF分别与x轴相交于G、H两点，且∠PGH=∠PHG，求直线EF的斜率．
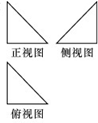若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形，则这个空间几何体的外接球的表面积（　　）
A、3B、3πC、9D、9π
已知曲线C1的参数方程为
x=2+2cosα
y=2sinα
（α为参数）．在平面直角坐标系中，以坐
标原点为极点，x轴的非负半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρcos（θ+
π
4
）=2
2
．
（Ⅰ）把C1的参数方程化为极坐标方程；
（Ⅱ）求C1与C2交点的极坐标（ρ≥0，0≤θ＜2π）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网