题目内容
已知向量
，
是夹角为
的两个单位向量，
=2
+
，
=k
+2
，
（1）若
⊥
，求实数k的值；
（2）若k=-3，求
与
的夹角θ．
| e1 |
| e2 |
| π |
| 3 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
（1）若
| a |
| b |
（2）若k=-3，求
| a |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：（1）运用向量的数量积的定义和向量垂直的条件：数量积为0，解方程即可得到k；
（2）运用向量的夹角公式，首先分别求出向量a，b的模和数量积，计算即可得到．
（2）运用向量的夹角公式，首先分别求出向量a，b的模和数量积，计算即可得到．
解答：
解：（1）
•
=|
|•|
|•cos
=
，
若
⊥
，则
•
=0，
即（2
+
）•（k
+2
）=0，
即有2k
2+2
2+（k+4）
•
=2k+2+
（k+4）=0，
解得k=-
；
（2）若k=-3，则
•
=-6
2+2
2+（-3+4）
•
=-6+2+
=-
，
|
|2=4
2+
2+4
•
=4+1+2=7，
|
|2=9
2+4
2-12
•
=9+4-6=7，
则cosθ=
=
=-
，
由0≤θ≤π，解得θ=
．
| e1 |
| e2 |
| e1 |
| e2 |
| π |
| 3 |
| 1 |
| 2 |
若
| a |
| b |
| a |
| b |
即（2
| e1 |
| e2 |
| e1 |
| e2 |
即有2k
| e1 |
| e2 |
| e1 |
| e2 |
| 1 |
| 2 |
解得k=-
| 8 |
| 5 |
（2）若k=-3，则
| a |
| b |
| e1 |
| e2 |
| e1 |
| e2 |
| 1 |
| 2 |
| 7 |
| 2 |
|
| a |
| e1 |
| e2 |
| e1 |
| e2 |
|
| b |
| e1 |
| e2 |
| e1 |
| e2 |
则cosθ=
| ||||
|
|
-
| ||||
|
| 1 |
| 2 |
由0≤θ≤π，解得θ=
| 2π |
| 3 |
点评：本题考查向量的数量积的定义和性质，主要考查向量垂直的条件，以及向量的夹角的求法，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知某几何体的三视图如图所示，则它的体积是（ ）
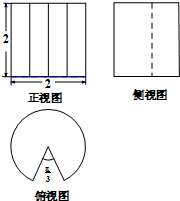
A、
| ||
B、
| ||
| C、π | ||
D、
|
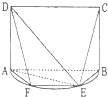如图，E是以AB为直径的半圆O上异于点A，B的点，边长为4的正方形ABCD所在的平面垂直于该半圆所在的平面．