题目内容
已知m∈（b，a），且m≠0，
的取值范围是（
，
），则实数a，b满足 ．
| 1 |
| m |
| 1 |
| a |
| 1 |
| b |
考点：不等式的基本性质
专题：不等式的解法及应用
分析：利用不等式的基本性质即可得出．
解答：
解：∵m∈（b，a），且m≠0，
的取值范围是（
，
），
∴0＜
＜
，或
＜
＜0，
∴a＞b＞0，或b＜a＜0，
故答案为：a＞b＞0或b＜a＜0．
| 1 |
| m |
| 1 |
| a |
| 1 |
| b |
∴0＜
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
∴a＞b＞0，或b＜a＜0，
故答案为：a＞b＞0或b＜a＜0．
点评：本题考查了不等式的基本性质，属于基础题．
练习册系列答案
相关题目
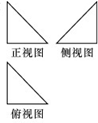若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形，则这个空间几何体的外接球的表面积（ ）| A、3 | B、3π | C、9 | D、9π |
正项等比数列{an}中，若log2（a1a9）=4，则a3a7等于（ ）
| A、16 | B、-16 |
| C、10 | D、256 |