题目内容
求证:(1-tanα)=(cos2α-cotα)(sec2α+tanα).
考点:三角函数恒等式的证明
专题:证明题
分析:首先要证明等式(1-tanα)=(cos2α-cotα)(sec2α+1tanα),就必须了解各种三角函数之间的转化关系,然后把它们都换成正余弦函数的形式,再求证.
解答:
解:等式左边:(1-tanα)=1-
=
..
等式的右边(cos2α-cotα)(sec2α+tanα)=(cos2α-
)(
+
)=
.
所以左边等于右边,
故(1-tanα)=(cos2α-cotα)(sec2α+tanα)成立.
| sinα |
| cosα |
| cosα-sinα |
| cosα |
等式的右边(cos2α-cotα)(sec2α+tanα)=(cos2α-
| cosα |
| sinα |
| 1 |
| cos2α |
| sinα |
| coaα |
| cosα-sinα |
| cosα |
所以左边等于右边,
故(1-tanα)=(cos2α-cotα)(sec2α+tanα)成立.
点评:此题主要考查三角函数恒等式的证明问题,其中运用到各种三角函数间的转化关系,在做题的时候要把它们转化统一再求证.属于中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
设函数f(x)=
x3-mx2+(m2-4)x,x∈R,当m=3时,则曲线y=f(x)在点(2,f(2))处的切线方程为( )
| 1 |
| 3 |
| A、9x+3y-20=0 |
| B、9x+3y-2=0 |
| C、9x+3y-10=0 |
| D、9x+3y+20=0 |
直线l与平面a内的两条直线都垂直,则直线l与平面a的位置关系是( )
| A、平行 | B、垂直 |
| C、在平面a内 | D、无法确定 |
a≥0,b≥0,a+b=1,且x1,x2为正数,y1=ax1+bx2,y2=bx1+ax2,则y1y2与x1x2的大小关系是( )
| A、y1y2≥x1x2 |
| B、y1y2≤x1x2 |
| C、y1y2>x1x2 |
| D、y1y2<x1x2 |
 ,其中常数
,其中常数 .
.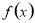 的单调区间及单调性;
的单调区间及单调性;  时
时 恒成立,求实数
恒成立,求实数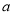 的取值范围.
的取值范围.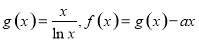 .
.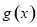 的单调区间;
的单调区间; 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值; ,使
,使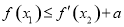 成立,求实数a的取值范围.
成立,求实数a的取值范围.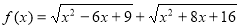 .
.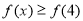 的解集;
的解集;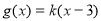 ,
,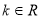 ,若
,若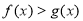 对任意的
对任意的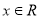 都成立,求实数
都成立,求实数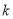 的取值范围.
的取值范围.