题目内容
(本题满分14分)已知函数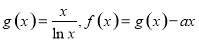 .
.
(1)求函数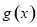 的单调区间;
的单调区间;
(2)若函数 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;
(3)若 ,使
,使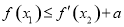 成立,求实数a的取值范围.
成立,求实数a的取值范围.
(1)单调减区间是 ,增区间是
,增区间是 ;(2)
;(2) ;(3)
;(3)
【解析】
试题分析:【解析】
由已知函数 的定义域均为
的定义域均为 ,且
,且 . 1分
. 1分
(1)函数 ,
,
当 且
且 时,
时, ;当
;当 时,
时, .
.
所以函数 的单调减区间是
的单调减区间是 ,增区间是
,增区间是 . 4分
. 4分
(2)因f(x)在 上为减函数,故
上为减函数,故 在
在 上恒成立.
上恒成立.
所以当 时,
时, .
.
又
 ,
,
故当 ,即
,即 时,
时, .
.
所以 于是
于是 ,故a的最小值为
,故a的最小值为 . 7分
. 7分
(3)命题“若 使
使 成立”等价于
成立”等价于
“当 时,有
时,有 ”.
”.
由(2),当 时,
时, ,
,
 .
.
问题等价于:“当 时,有
时,有 ”. 9分
”. 9分
 当
当 时,由(2),
时,由(2), 在
在 上为减函数,
上为减函数,
则 =
= ,故
,故 .
.
 当
当 时,由于
时,由于
 在
在 上为增函数,
上为增函数,
故 的值域为
的值域为 ,即
,即 .
.
(i)若 ,即
,即 ,
, 在
在 恒成立,故
恒成立,故 在
在 上为增函数,
上为增函数,
于是, =
= ,不合题意. 11分
,不合题意. 11分
(ii)若 ,即
,即 ,由
,由 的单调性和值域知,
的单调性和值域知,
 唯一
唯一 ,使
,使 ,且满足:
,且满足:
当 时,
时, ,
, 为减函数;当
为减函数;当 时,
时, ,
, 为增函数;
为增函数;
所以, =
= ,
, .
.
所以, ,与
,与 矛盾,不合题意.
矛盾,不合题意.
综上,得 . 14分
. 14分
考点:本题考查利用导数研究函数的单调性,利用导数研究函数的最值问题

练习册系列答案
相关题目
设ξ的概率密度函数为f(x)=
e-
,则下列结论错误的是( )
| 1 | ||
|
| (x-1)2 |
| 2 |
| A、p(ξ<1)=p(ξ>1) |
| B、p(-1≤ξ≤1)=p(-1<ξ<1) |
| C、f(x)的渐近线是x=0 |
| D、η=ξ-1~N(0,1) |
 中,角
中,角 的对边分别是
的对边分别是 ,若
,若 的面积为
的面积为 ,则
,则 ;
;
 的图象向左平移
的图象向左平移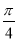 个单位,再向上平移1个单位,所得图象的函数解析式是( )
个单位,再向上平移1个单位,所得图象的函数解析式是( )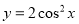 (B)
(B)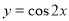
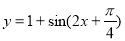 (D)
(D)
 =sin(2x+
=sin(2x+ )+ cos 2x.
)+ cos 2x.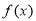 的单调递增区间。
的单调递增区间。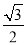 ,a=2,B=
,a=2,B=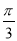 ,求△ABC的面积.
,求△ABC的面积. ,不等式
,不等式 恒成立,则一定有( )
恒成立,则一定有( ) B.
B.
 D.
D.
 的最小值是_____________
的最小值是_____________ 表示二进制的数,将它转换成二进制的形式是
表示二进制的数,将它转换成二进制的形式是 ,那么将二进制数
,那么将二进制数 转换成十进制的形式是( )
转换成十进制的形式是( ) B.
B. C.
C. D.
D.