题目内容
已知正三棱锥P-ABC中,E、F分别是AC,PC的中点,若EF⊥BF,AB=2,则三棱锥P-ABC的外接球的表面积为 .
考点:球的体积和表面积
专题:球
分析:证明以PA、PB、PC为从同一点P出发的正方体三条棱,将此三棱锥补成正方体,则它们有相同的外接球,正方体的体对角线就是外接球的直径,求出半径即可求解球的表面积.
解答:
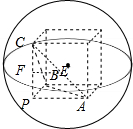 解:∵E、F分别是AC,PC的中点,∴EF∥PA,
解:∵E、F分别是AC,PC的中点,∴EF∥PA,
∵P-ABC是正三棱锥,
∴PA⊥BC(对棱垂直),
∴EF⊥BC,又EF⊥BF,而BF∩BC=B,
∴EF⊥平面PBC,
∴PA⊥平面PBC,
∴∠APB=∠APC=∠BPC=90°,
以PA、PB、PC为从同一点P出发的正方体三条棱,将此三棱锥补成正方体,则它们有相同的外接球,
正方体的体对角线就是外接球的直径,
又AB=2,∴PA=
,
∴2R=
PA=
,
∴R=
,
∴三棱锥P-ABC的外接球的表面积为:4πR2=4π×(
)2=6π.
故答案为:6π.
 解:∵E、F分别是AC,PC的中点,∴EF∥PA,
解:∵E、F分别是AC,PC的中点,∴EF∥PA,∵P-ABC是正三棱锥,
∴PA⊥BC(对棱垂直),
∴EF⊥BC,又EF⊥BF,而BF∩BC=B,
∴EF⊥平面PBC,
∴PA⊥平面PBC,
∴∠APB=∠APC=∠BPC=90°,
以PA、PB、PC为从同一点P出发的正方体三条棱,将此三棱锥补成正方体,则它们有相同的外接球,
正方体的体对角线就是外接球的直径,
又AB=2,∴PA=
| 2 |
∴2R=
| 3 |
| 6 |
∴R=
| ||
| 2 |
∴三棱锥P-ABC的外接球的表面积为:4πR2=4π×(
| ||
| 2 |
故答案为:6π.
点评:本题考查几何体的外接球的表面积的求法,判断几何体与球的关系,求出球的半径是解题的关键.

练习册系列答案
相关题目
已知变量x,y满足约束条件
,则z=4x+y的最小值为( )
|
| A、55 | B、-55 | C、5 | D、-5 |
设向量
,
不共线,
=3(
+
),
=
-
,
=2
+
,给出下列结论:
①A,B,C共线;
②A,B,D共线;
③B,C,D共线;
④A,C,D共线,
其中所有正确结论的序号为 .
| e1 |
| e2 |
| AB |
| e1 |
| e2 |
| CB |
| e2 |
| e1 |
| CD |
| e1 |
| e2 |
①A,B,C共线;
②A,B,D共线;
③B,C,D共线;
④A,C,D共线,
其中所有正确结论的序号为
设集合S={0,a},T={x∈Z|x2<2},则“a=1”是“S⊆T”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
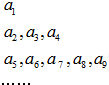 将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.
将数列{an}中的所有项按每一行比上一行多两项的规则排列成如图数表,已知图中的第一列数a1,a2,a5…构成一个等差数列,记为数列{bn},且b2=4,b5=10,图中每一行正中间一个数a1,a3,a7…构成数列{cn},其前n项和为Sn.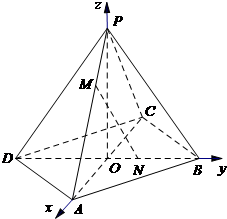 如图,在空间直角坐标系O-xyz中,正四棱锥P-ABCD的侧棱长与底边长都为
如图,在空间直角坐标系O-xyz中,正四棱锥P-ABCD的侧棱长与底边长都为