题目内容
 某市调研机构对该市工薪阶层对“楼市限购令”态度进行调查,抽调了50名市民,他们月收入频数分布表和对“楼市限购令”赞成人数如下表:
某市调研机构对该市工薪阶层对“楼市限购令”态度进行调查,抽调了50名市民,他们月收入频数分布表和对“楼市限购令”赞成人数如下表:| 月收入(单位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | c | 10 | 5 | 5 | |
| 频率 | 0.1 | a | b | 0.2 | 0.1 | 0.1 |
| 赞成人数 | 4 | 8 | 12 | 5 | 3 | 1 |
(Ⅱ)若从收入(单位:百元)在[55,65)的被调查者中随机选取两人进行追踪调查,求选中的2人至少有1人不赞成“楼市限购令”的概率.
考点:列举法计算基本事件数及事件发生的概率,频率分布直方图
专题:概率与统计
分析:(Ⅰ)由于所抽调的50名市民中,收入在[35,45)的有15名,可得到b的值,再由频率之和为1,即可得到a的值,进而得到c的值,根据频数分布表中的数据,即可得到频率分布直方图;
(Ⅱ)设月收入在55,65的5人编号,列出任取2人共10种结果,含有不赞成的共7种情况,根据古典概型的公式进行求解即可.
(Ⅱ)设月收入在55,65的5人编号,列出任取2人共10种结果,含有不赞成的共7种情况,根据古典概型的公式进行求解即可.
解答:
解:(I)由频率分布表得0.1+a+b+0.2+0.1+0.1=1,
即a+b=0.5.
因为所抽调的50名市民中,收入(单位:百元)在[35,45)的有15名,
所以b=
=0.3,
所以a=0.2,c=0.2×50=10,
所以a=0.2,b=0.3,c=10,
且频率分布直方图如下:
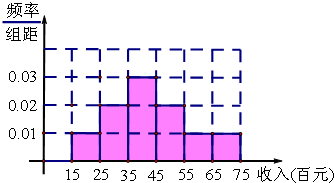
(II)设收入(单位:百元)在[55,65)的被调查者中赞成的分别是A1,A2,A3,不赞成的分别是B1,B2,
事件M:选中的2人中至少有1人不赞成“楼市限购令”,
则从收入(单位:百元)在[55,65)的被调查者中,任选2名的基本事件共有10个:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),
(A2,A3),(A2,B1),(A2,B2),
(A3,B1),(A3,B2),(B1,B2)
事件M包含的结果是(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2)共7个,
所以P(M)=
,
故所求概率为
.
即a+b=0.5.
因为所抽调的50名市民中,收入(单位:百元)在[35,45)的有15名,
所以b=
| 15 |
| 50 |
所以a=0.2,c=0.2×50=10,
所以a=0.2,b=0.3,c=10,
且频率分布直方图如下:

(II)设收入(单位:百元)在[55,65)的被调查者中赞成的分别是A1,A2,A3,不赞成的分别是B1,B2,
事件M:选中的2人中至少有1人不赞成“楼市限购令”,
则从收入(单位:百元)在[55,65)的被调查者中,任选2名的基本事件共有10个:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),
(A2,A3),(A2,B1),(A2,B2),
(A3,B1),(A3,B2),(B1,B2)
事件M包含的结果是(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2)共7个,
所以P(M)=
| 7 |
| 10 |
故所求概率为
| 7 |
| 10 |
点评:本题考查频率分布直方图,考查古典概率的计算,考查学生的阅读与计算能力,属于中档题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
的图象大致是( )
| x3 |
| 2x-1 |
A、 |
B、 |
C、 |
D、 |
若α是第四象限角,则( )
| A、sinα>tanα |
| B、sinα<tanα |
| C、sinα≥tanα |
| D、以上都不对 |
已知复数z=
(其中i为虚数单位),则复数z的共轭复数
等于( )
| 3+4i |
| 1-2i |
. |
| z |
| A、-1-2i | B、-1+2i |
| C、1+2i | D、1-2i |
设随机变量a服从正态分布N(u,9),若p(ξ>3)=p(ξ<1),则u=( )
| A、2 | B、3 | C、9 | D、1 |