题目内容
已知复数z=
(其中i为虚数单位),则复数z的共轭复数
等于( )
| 3+4i |
| 1-2i |
. |
| z |
| A、-1-2i | B、-1+2i |
| C、1+2i | D、1-2i |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数的运算法则、共轭复数的定义即可得出.
解答:
解:复数z=
=
=
=-1+2i,
则复数z的共轭复数
=-1-2i.
故选:A.
| 3+4i |
| 1-2i |
| (3+4i)(1+2i) |
| (1-2i)(1+2i) |
| -5+10i |
| 5 |
则复数z的共轭复数
. |
| z |
故选:A.
点评:本题考查了复数的运算法则、共轭复数的定义,属于基础题.

练习册系列答案
相关题目
复数z=
(其中i为虚数单位)在复平面内对应的点所在的象限为( )
| 3-i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设等差数列{an}的前n项和为Sn,且S3=6,a1=4,则公差d等于( )
| A、-2 | ||
| B、1 | ||
C、
| ||
| D、3 |
已知A={x|x2-4x-5=0},B={x|x2=1},则A∩B=( )
| A、{1} |
| B、{1,-1,5} |
| C、{-1} |
| D、{1,-1,-5} |
经过圆x2-2x+y2=0的圆心且与直线x+2y=0平行的直线方程是( )
| A、x+2y-1=0 |
| B、x-2y-2=0 |
| C、x-2y+1=0 |
| D、x+2y+2=0 |
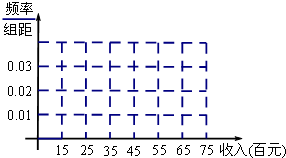 某市调研机构对该市工薪阶层对“楼市限购令”态度进行调查,抽调了50名市民,他们月收入频数分布表和对“楼市限购令”赞成人数如下表:
某市调研机构对该市工薪阶层对“楼市限购令”态度进行调查,抽调了50名市民,他们月收入频数分布表和对“楼市限购令”赞成人数如下表: