题目内容
某企业最近四年的年利润呈上升趋势,通过统计,前三年的年利润增长数相同,后两年的年利润增长率相同,已知第一年的年利润为3千万元,第四年的年利润为6.25千万元,则该企业这四年的平均年利润为 千万元.
考点:函数模型的选择与应用
专题:函数的性质及应用
分析:根据前三年的利润增长率相同,后两年的年增长率相同,建立方程关系进行求解即可.
解答:
解:设前三年的年利润增长数为x,
则前四年的利润分别为3,3+x,3+2x,6.25,
∵后两年的年利润增长率相同,设增长率为p,
∴
,
两式相除得
=
,
整理得16x2+23x-39=0,
即(x-1)(16x+39)=0,
解得x=1或x=-
(舍),
则前4年的利润分别为3,4,5,
,
则四年的平均利润为
=
=4.5625(千万元),
故答案为:
或4.5625.
则前四年的利润分别为3,3+x,3+2x,6.25,
∵后两年的年利润增长率相同,设增长率为p,
∴
|
两式相除得
| 3+x |
| 3+2x |
| 3+2x | ||
|
整理得16x2+23x-39=0,
即(x-1)(16x+39)=0,
解得x=1或x=-
| 39 |
| 16 |
则前4年的利润分别为3,4,5,
| 25 |
| 4 |
则四年的平均利润为
3+4+5+
| ||
| 4 |
| 73 |
| 16 |
故答案为:
| 73 |
| 16 |
点评:本题主要考查函数的应用问题,利用增长率之间的关系,建立方程求出增长数是解决本题的关键.

练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn,且S3=6,a1=4,则公差d等于( )
| A、-2 | ||
| B、1 | ||
C、
| ||
| D、3 |
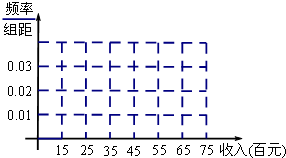 某市调研机构对该市工薪阶层对“楼市限购令”态度进行调查,抽调了50名市民,他们月收入频数分布表和对“楼市限购令”赞成人数如下表:
某市调研机构对该市工薪阶层对“楼市限购令”态度进行调查,抽调了50名市民,他们月收入频数分布表和对“楼市限购令”赞成人数如下表: