��Ŀ����
����һ������{an}��������������ȡm��m��3��m��N*������Ҳ��ı�����������{an}�е��Ⱥ���õ�������{an}��һ��m�������У�
��֪����{an}��ͨ�ʽΪan=
��n��N*��aΪ���������Ȳ�����a2��a3��a6������{an}��һ��3�ӽ����У�
��1����a��ֵ��
��2���Ȳ�����b1��b2������bm��{an}��һ��m��m��3��m��N*���������У���b1=
��kΪ������k��N*��k��2������֤��m��k+1
��3���ȱ�����c1��c2������cm��{an}��һ��m��m��3��m��N*���������У���֤��c1+c1+��+cm��2-
��
��֪����{an}��ͨ�ʽΪan=
| 1 |
| n+a |
��1����a��ֵ��
��2���Ȳ�����b1��b2������bm��{an}��һ��m��m��3��m��N*���������У���b1=
| 1 |
| k |
��3���ȱ�����c1��c2������cm��{an}��һ��m��m��3��m��N*���������У���֤��c1+c1+��+cm��2-
| 1 |
| 2m-1 |
���㣺���е����,�Ȳ����е�����
ר�⣺�Ȳ�������ȱ�����
��������1�����õȲ����еĶ��弰�����ʼ��ɵó���
��2����Ȳ�����b1��b2������bm�Ĺ���Ϊd����b1=
���ɵ�b2��
�������õȲ����е�ͨ�ʽ���䲻��ʽ�����ʼ���֤����
��3����c1=
��t��N*�����ȱ�����c1��c2������cm�Ĺ���Ϊq����c2��
���ɵ�q=
��
���Ӷ�cn=c1qn-1��
(
)n-1��1��n��m��n��N*���������õȱ����е�ǰn���ʽ�������ĵ����Լ��ɵó���
��2����Ȳ�����b1��b2������bm�Ĺ���Ϊd����b1=
| 1 |
| k |
| 1 |
| k+1 |
��3����c1=
| 1 |
| t |
| 1 |
| t+1 |
| c2 |
| c1 |
| t |
| t+1 |
| 1 |
| t |
| t |
| t+1 |
���
��1���⣺��a2��a3��a6�ɵȲ����У�
��a2-a3=a3-a6��
�֡�a2=
��a3=
��a6=
��
�����
-
=
-
�����a=0��
��2��֤������Ȳ�����b1��b2������bm�Ĺ���Ϊd��
��b1=
����b2��
��
�Ӷ�d=b2-b1��
-
=-
��
��bm=b1+��m-1��d��
-
��
�֡�bm��0����
-
��0��
��m-1��k+1��
��m��k+2��
�֡�m��k��N*����m��k+1��
��3��֤������c1=
��t��N*�����ȱ�����c1��c2������cm�Ĺ���Ϊq��
��c2��
����q=
��
��
�Ӷ�cn=c1qn-1��
(
)n-1��1��n��m��n��N*����
��c1+c2+��+cm��
+
(
)1+
(
)2+��+
(
)m-1
=
[1-(
)m]��
�躯��f��x��=x-
����m��3��m��N*����
��x�ʣ�0��+�ޣ�ʱ������f��x��=x-
������������
�ߵ�t��N*����1��
��2����f��
����2-
��
�� c1+c2+��+cm��2-
��
��a2-a3=a3-a6��
�֡�a2=
| 1 |
| 2+a |
| 1 |
| 3+a |
| 1 |
| 6+a |
�����
| 1 |
| 2+a |
| 1 |
| 3+a |
| 1 |
| 3+a |
| 1 |
| 6+a |
��2��֤������Ȳ�����b1��b2������bm�Ĺ���Ϊd��
��b1=
| 1 |
| k |
| 1 |
| k+1 |
�Ӷ�d=b2-b1��
| 1 |
| k+1 |
| 1 |
| k |
| 1 |
| k(k+1) |
��bm=b1+��m-1��d��
| 1 |
| k |
| m-1 |
| k(k+1) |
�֡�bm��0����
| 1 |
| k |
| m-1 |
| k(k+1) |
��m-1��k+1��
��m��k+2��
�֡�m��k��N*����m��k+1��
��3��֤������c1=
| 1 |
| t |
��c2��
| 1 |
| t+1 |
| c2 |
| c1 |
| t |
| t+1 |
�Ӷ�cn=c1qn-1��
| 1 |
| t |
| t |
| t+1 |
��c1+c2+��+cm��
| 1 |
| t |
| 1 |
| t |
| t |
| t+1 |
| 1 |
| t |
| t |
| t+1 |
| 1 |
| t |
| t |
| t+1 |
=
| t+1 |
| t |
| t |
| t+1 |
�躯��f��x��=x-
| 1 |
| xm-1 |
��x�ʣ�0��+�ޣ�ʱ������f��x��=x-
| 1 |
| xm-1 |
�ߵ�t��N*����1��
| t+1 |
| t |
| t+1 |
| t |
| 1 |
| 2m-1 |
�� c1+c2+��+cm��2-
| 1 |
| 2m-1 |
���������⿼�������õȱ�������Ȳ����е�ͨ�ʽ����ǰn���ʽ�������ĵ����ԡ�����ʽ�����ʣ���������������������������������⣮

��ϰ��ϵ�д�
�����Ŀ
����z=
������iΪ������λ���ڸ�ƽ���ڶ�Ӧ�ĵ����ڵ�����Ϊ��������
| 3-i |
| 1+i |
| A����һ���� | B���ڶ����� |
| C���������� | D���������� |
��֪A={x|x2-4x-5=0}��B={x|x2=1}����A��B=��������
| A��{1} |
| B��{1��-1��5} |
| C��{-1} |
| D��{1��-1��-5} |
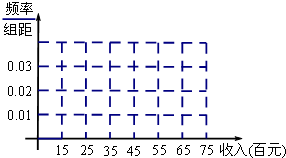 ij�е��л����Ը��й�н�ײ�ԡ�¥�����̬�Ƚ��е��飬�����50����������������Ƶ���ֲ����Ͷԡ�¥��������������±���
ij�е��л����Ը��й�н�ײ�ԡ�¥�����̬�Ƚ��е��飬�����50����������������Ƶ���ֲ����Ͷԡ�¥��������������±���