Question

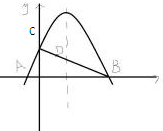如图，抛物线y=ax²+bx+6与x轴交于AB两点与y轴交点C，已知A（-1，0）、B（3，0）．
（1）求抛物线及直线BC的解析式；
（2）若P为抛物线上位于直线BC上方的一点，求△PBC面积S的最大值并求出此时点P的坐标．
（3）直线BC与抛物线的对称轴交于点D，M为抛物线上一动点，点N在x轴上，若以点DAMN为顶点的四边形是平行四边形，求出所有满足条件的点M．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）由于抛物线y=ax²+bx+6与x轴交于A，B两点，可得-1，3是一元二次方程ax²+bx+6=0的两个实数根，利用根与系数的关系可得a，b，可得抛物线的解析式，令x=0，即可得出点C的纵坐标．
（2）设过点P的抛物线的与直线BC平行的切线方程为2x+y+m=0．与抛物线的方程联立可得2x²-6x-6-m=0，令△=0，解得m，即可得出P点坐标．利用点到直线的距离公式可得点P到直线BC的距离h．又|BC|=

32+62

=3

5

．可得△PBC面积S的最大值=

1

2

×|BC|×h．
（3）抛物线的对称轴x=1，代入直线BC的方程可得y=4，可得D（1，4）．设N（n，0），M（x，-2x²+4x+6），则

AD

=（2，4），

MN

=（n-x，2x²-4x-6）．
∵以点DAMN为顶点的四边形是平行四边形，可得

AD

=

MN

，利用向量相等即可得出．

解答： 解：（1）∵抛物线y=ax²+bx+6与x轴交于A，B两点，
∴-1，3是一元二次方程ax²+bx+6=0的两个实数根，
∴

-1+3=- b a -1×3= 6 a

，解得a=-2，b=4．
∴抛物线的方程为y=-2x²+4x+6，
令x=0，可得y_C=6．
∴C（0，6），
∴直线BC的方程为

x

3

+

y

6

=1，化为 2x+y-6=0．
（2）设过点P的抛物线的与直线BC平行的切线方程为2x+y+m=0．
联立

2x+y+m=0 y=-2x2+4x+6

，化为2x²-6x-6-m=0，
令△=36-8（-6-m）=0，解得m=-

21

2

．
代入上述方程可得2x²-6x-6+

21

2

=0，
化为（2x-3）²=0，解得x=

3

2

，
∴y=-2×

3

2

-(-

21

2

)=

15

2

．
∴P(

3

2

，

15

2

)．
点P到直线BC的距离h=

|2× 3 2 + 15 2 -6|

22+1

=

9 5

10

．
又|BC|=

32+62

=3

5

．
∴△PBC面积S的最大值=

1

2

×|BC|×h=

1

2

×3

5

×

9 5

10

=

27

4

．
（3）抛物线的对称轴x=1，代入直线BC的方程可得y=4，∴D（1，4）．
设N（n，0），M（x，-2x²+4x+6），
则

AD

=（2，4），

MN

=（n-x，2x²-4x-6）．
∵以点DAMN为顶点的四边形是平行四边形，
∴

AD

=

MN

，
∴

2=n-x 4=2x2-4x-6

，解得

x=1+ 6 n=3+ 6

或

x=1- 6 n=3- 6

．
∴M(1+

6

，-4)或(1-

6

，-4)．

点评：本题了考查了抛物线的方程及其性质、抛物线的切线、三角形的面积最大值、点到直线的距离公式、平行四边形的性质、向量相等，考查了推理能力与计算能力，属于难题．