题目内容
下列命题
①“若x+y=0，则x，y互为相反数”的逆命题；
②“若a＞b，则a2＞b2”的逆否命题；
③“若x≤-3，则x2+x-6≥0”的否命题．
其中真命题个数为（ ）
①“若x+y=0，则x，y互为相反数”的逆命题；
②“若a＞b，则a2＞b2”的逆否命题；
③“若x≤-3，则x2+x-6≥0”的否命题．
其中真命题个数为（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：命题的真假判断与应用
专题：简易逻辑
分析：利用四种命题定义及其之间的关系即可得出．
解答：
解：①“若x+y=0，则x，y互为相反数”的逆命题为：“若x，y互为相反数，则x+y=0”正确；
②“若a＞b，则a2＞b2”的逆否命题为：“若a2≤b2，则a＜b”，不正确；
③“若x≤-3，则x2+x-6≥0”的否命题为：“③“若x＞-3，则x2+x-6＜0”不正确．
综上可知：只有①．
故选：B．
②“若a＞b，则a2＞b2”的逆否命题为：“若a2≤b2，则a＜b”，不正确；
③“若x≤-3，则x2+x-6≥0”的否命题为：“③“若x＞-3，则x2+x-6＜0”不正确．
综上可知：只有①．
故选：B．
点评：本题考查了四种命题定义及其之间的关系，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
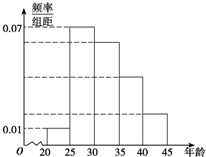如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图，现已知年龄在[30，35）、[35，40）、[40，45]的上网人数呈现递减的等差数列分布，则年龄在[35，40）的网民出现的频率为（ ）| A、0.04 | B、0.06 |
| C、0.2 | D、0.3 |
复数(
)2=（ ）
| 2i |
| 1+i |
| A、2i | B、-2i | C、2 | D、-2 |
若数列{an}的前n项和为Sn，有下列命题：
（1）若数列{an}的极限存在但不为零，则数列{Sn}的极限一定不存在；
（2）无穷数列{S2n}、{S2n-1}的极限均存在，则数列{Sn}的极限一定存在；
（3）若{an}是等差数列（公差d≠0），则S1•S2•…•Sk=O的充要条件是a1•a2•…•ak=O；
（4）若{an}是等比数列，则S1•S2•…•Sk=O（k≥2）的充要条件是an+an+1=0．
其中，错误命题的序号是（ ）
（1）若数列{an}的极限存在但不为零，则数列{Sn}的极限一定不存在；
（2）无穷数列{S2n}、{S2n-1}的极限均存在，则数列{Sn}的极限一定存在；
（3）若{an}是等差数列（公差d≠0），则S1•S2•…•Sk=O的充要条件是a1•a2•…•ak=O；
（4）若{an}是等比数列，则S1•S2•…•Sk=O（k≥2）的充要条件是an+an+1=0．
其中，错误命题的序号是（ ）
| A、（1）（2） |
| B、（2）（3） |
| C、（3）（4） |
| D、（1）（4） |
已知直线x=a（a＜0）与函数y=（
） x，y=(
)x，y=2x，y=10x的图象依次交与A，B，C，D四点，则这四个点从上到下的排列次序是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、A、B、C、D |
| B、B、C、A、D |
| C、B、A、C、D |
| D、C、A、B、D |
下列函数中，与函数f(x)=
的奇偶性、单调性均相同的是（ ）
| ex-e-x |
| 3 |
A、y=ln(x+
| ||
| B、y=x2 | ||
| C、y=tanx | ||
| D、y=ex |