题目内容
6.若f(x)=$\frac{1}{{\sqrt{x+1}}},g(x)=\frac{{\sqrt{x+1}}}{x-2}$,则f(x)•g(x)=$\frac{1}{x-2},x∈(-1,2)∪(2,+∞)$.分析 先求出函数的定义域,然后根据函数表达式进行化简求解即可.
解答 解:要使函数f(x)有意义,则x+1>0,即x>-1,
要使函数g(x)有意义,则$\left\{\begin{array}{l}{x+1≥0}\\{x-2≠0}\end{array}\right.$,即$\left\{\begin{array}{l}{x≥-1}\\{x≠2}\end{array}\right.$,即x≥-1且x≠2,
要使f(x)•g(x)有意义,则$\left\{\begin{array}{l}{x>-1}\\{x≥-1且x≠2}\end{array}\right.$,
即x>-1且x≠2,即函数的定义域为(-1,2)∪(2,+∞),
则f(x)•g(x)=$\frac{1}{\sqrt{x+1}}$•$\frac{\sqrt{x+1}}{x-2}$=$\frac{1}{x-2},x∈(-1,2)∪(2,+∞)$,
故答案为:$\frac{1}{x-2},x∈(-1,2)∪(2,+∞)$
点评 本题主要考查函数解析式的求解,注意要求函数的定义域.

练习册系列答案
相关题目
19.已知cos2α=$\frac{1}{3}$,则$\frac{tan2α}{tanα}$的值为( )
| A. | -4 | B. | -$\frac{1}{4}$ | C. | 4 | D. | $\frac{1}{4}$ |
1.过平面外的一条直线,且与平面垂直的平面有( )
| A. | 一个 | B. | 无数个 | C. | 不存在 | D. | 一个或无数个 |
11.函数$y=\frac{{\sqrt{x}}}{x-1}$的定义域为( )
| A. | [0,1)∪(1,+∞) | B. | (0,+∞) | C. | (0,1) | D. | [0,1] |
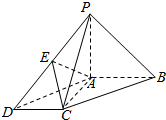 在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.
在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点. 如图,直三陵柱ABC-A1B1C1中,△ABC为等腰直角三角形,AC=BC=1,AA1=$\sqrt{2}$,D是A1B1的中点,F是B1B上一点.
如图,直三陵柱ABC-A1B1C1中,△ABC为等腰直角三角形,AC=BC=1,AA1=$\sqrt{2}$,D是A1B1的中点,F是B1B上一点.