到一个角的两边距离相等的点都在_________。
 这个角的平分线上
【解析】根据定义可知:到一个角的两边距离相等的点在这个角的平分线上、角平分线上的点到这个角的两边的距离相等。
这个角的平分线上
【解析】根据定义可知:到一个角的两边距离相等的点在这个角的平分线上、角平分线上的点到这个角的两边的距离相等。 ∠AOB的平分线上一点M ,M到 OA的距离为1.5 cm,则M到OB的距离为_________。
 1.5cm
【解析】∵M是∠AOB的平分线上一点,
∴点M到OB的距离等于M到OA的距离,
∴M到OB的距离为1.5cm.
故答案为:1.5cm.
1.5cm
【解析】∵M是∠AOB的平分线上一点,
∴点M到OB的距离等于M到OA的距离,
∴M到OB的距离为1.5cm.
故答案为:1.5cm. 如图,∠AOB=60°,PD⊥OA于D,PE⊥OB于E,且PD=PE,则∠1=________

 30°
【解析】由角平分逆定理可知:∠1=∠2=30°.
故的答案为30°.
30°
【解析】由角平分逆定理可知:∠1=∠2=30°.
故的答案为30°. 三角形的三条角平分线相交于一点,并且这一点到________________相等
 三边的距离
【解析】三角形三条角平分线的交点到三角形三条边的距离相等.
故答案为三边的距离.
三边的距离
【解析】三角形三条角平分线的交点到三角形三条边的距离相等.
故答案为三边的距离. 在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD∶CD=9∶7,则D到AB的距离为______
 18
【解析】试题分析:过点D作DE⊥AB,由BC=32,BD∶CD=9∶7,即可求得CD的长,再根据角平分线的性质即可求得结果.
过点D作DE⊥AB,
∵BD∶CD=9∶7,
∴CD=BC·=14
∵AD平分∠CAB,DE⊥AB,∠C=90°
∴DE=CD=14
18
【解析】试题分析:过点D作DE⊥AB,由BC=32,BD∶CD=9∶7,即可求得CD的长,再根据角平分线的性质即可求得结果.
过点D作DE⊥AB,
∵BD∶CD=9∶7,
∴CD=BC·=14
∵AD平分∠CAB,DE⊥AB,∠C=90°
∴DE=CD=14 如图,△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若DC=7,则点D到AB的距离DE= .
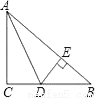
 7
【解析】试题分析: ∵∠C=90°,AD平分∠BAC,点D到AB的距离DE,∴DE=DC=7.故填7.
7
【解析】试题分析: ∵∠C=90°,AD平分∠BAC,点D到AB的距离DE,∴DE=DC=7.故填7. 到三角形三边距离相等的点叫做三角形的_________
 内心
【解析】到三角形三边距离相等的点为三角形三条角平分线的交点,叫做三角形的内心.
故答案为内心.
内心
【解析】到三角形三边距离相等的点为三角形三条角平分线的交点,叫做三角形的内心.
故答案为内心. 如图,在△ABC中,BC=5cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则△PDE的周长是 cm.
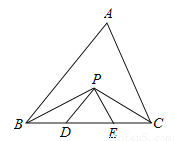
 5.
【解析】
试题分析:∵BP、CP分别是∠ABC和∠ACB的角平分线,∴∠ABP=∠PBD,∠ACP=∠PCE,∵PD∥AB,PE∥AC,∴∠ABP=∠BPD,∠ACP=∠CPE,∴∠PBD=∠BPD,∠PCE=∠CPE,∴BD=PD,CE=PE,∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=5cm.故答案为:5.
5.
【解析】
试题分析:∵BP、CP分别是∠ABC和∠ACB的角平分线,∴∠ABP=∠PBD,∠ACP=∠PCE,∵PD∥AB,PE∥AC,∴∠ABP=∠BPD,∠ACP=∠CPE,∴∠PBD=∠BPD,∠PCE=∠CPE,∴BD=PD,CE=PE,∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=5cm.故答案为:5. 已知:AC=AD,AB是∠CAD的角平分线,求证:BC=BD.
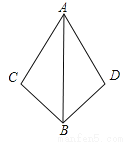
 证明见解析.
【解析】证明:∵AB是∠CAD的角平分线
∴∠BAC=∠BAD ……………………………………………1分
在△ABC和△ABD中
……………………………………3分
∴△ABC≌△ABD …………………………4分
∴BC=BD
证明见解析.
【解析】证明:∵AB是∠CAD的角平分线
∴∠BAC=∠BAD ……………………………………………1分
在△ABC和△ABD中
……………………………………3分
∴△ABC≌△ABD …………………………4分
∴BC=BD