题目内容
到三角形三边距离相等的点叫做三角形的_________
内心
【解析】到三角形三边距离相等的点为三角形三条角平分线的交点，叫做三角形的内心.
故答案为内心.
练习册系列答案
阅读快车系列答案
相关题目
若分式方程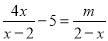
无解，那么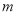
的值应为___________．
－8
【解析】试题解析： 分式方程无解，
把原方程去分母得：
把代入方程，得
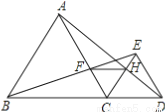
故答案为： 如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形.BE交AC于F，AD交CE于H，求证：
（1）△BCE≌△ACD；
（2）CF=CH；
（3）△FCH是等边三角形；
（4）FH∥BD.
见解析
【解析】试题分析：（1）由等边三角形的三边相等，三角都是60°，再根据平角的关系，就能证明△BCE≌△ACD；（2）由△BCE≌△ACD得出对应角相等，结合等边三角形的边角特点证明△BCF≌△ACH，能得出CF=CH；（3）两边等，加上一个角60°推出△CFH是等边三角形；（4）根据内错角相等，两直线平行推出FH∥BD.
试题解析：
证明：∵△ABC和△CDE都是等边三角... 在△ABC中，D是BC上的点，AB=AD=DC，∠B=70°，则∠C的度数为（ ）
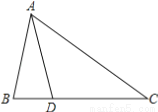
A. 35° B. 40° C. 45° D. 50°
A
【解析】∵AB=AD, ∴∠ADB=∠B=70°.
∵AD=DC，
∴35°.
故选A. 在△ABC中，AB=AC，BD是角平分线，BD=AD，求∠A的度数．
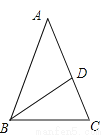
∠A=36°
【解析】试题分析：设∠A的度数为x°，由等腰三角形的性质分别表示出∠ABC和∠C的度数，再根据三角形内角和列方程求解即可.
试题解析：
设∠A=x°，
∵BD=AD，
∴∠A=∠ABD=x°，
∴∠BDC=∠A+∠ABD=2x°，
∵BD=BC，
∴∠BDC=∠BCD=2x°，
∵AB=AC，
∴∠ABC=∠BCD=2x°，... 如图，∠AOB=60°，PD⊥OA于D，PE⊥OB于E，且PD=PE，则∠1=________
30°
【解析】由角平分逆定理可知：∠1=∠2=30°.
故的答案为30°. 如图，在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于D，如果AC=3cm，那么AE+DE等于（ ）
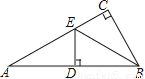
A. 2cm B. 3cm C. 4cm D. 5cm
B
【解析】试题分析：根据角平分线的性质，由BE平分∠ABC，∠ACB=90°，DE⊥AB，可得CE=DE，即可求得结AE+DE=AE+CE=AC=3cm.
故选B. 2（a2+b2）-（a+b）2
a2-2ab+b2
【解析】试题分析：先根据完全平方公式计算，再合并同类项即可.
试题解析：
2（a2+b2）-（a+b）2=2a2+2b2-a2-2ab-b2=a2-2ab+b2. (2y-3z)(2y+3z)等于（ ）
A. y2-z2 B. 2y2-3z2 C. 4y2-9z2 D. y2-z2
C
【解析】根据平方差公式可得：(2y-3z)(2y+3z)=4y2-9z2，故选C.