题目内容
三角形的三条角平分线相交于一点，并且这一点到________________相等
三边的距离
【解析】三角形三条角平分线的交点到三角形三条边的距离相等.
故答案为三边的距离.
练习册系列答案
相关题目
若分式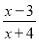
的值为0，则x的值是（ ）
A.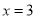 
B. 
C. 
D.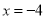 
A
【解析】根据题意可得： =0，方程两边同时乘以(x+4）得：x-3=0，解得：x=3；检验：将x=3代入x+4=7≠0，故x=3为原方程的解。
故本题正确答案为A。 在△ABC中，与∠A相邻的外角是100°，要使△ABC是等腰三角形，则∠B的度是_________.
80°或50°或20°
【解析】∵∠A的相邻外角是100°，∴∠A=80°．
分两种情况：
（1）当∠A为底角时，另一底角∠B=∠A=80°；
（2）当∠A为顶角时，则底角∠B=∠C= (180°?80°) =50°
（3）当∠B是顶角时，∠B=180°-2∠A=20°．
综上所述，∠B的度数是80°或50°或20°. 已知等腰三角形的两边长分别是3和5，则该三角形的周长是（ ）
A. 8 B. 9 C. 10或12 D. 11或13
D
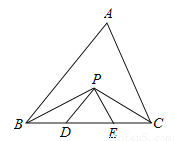
【解析】分两种情况：①当3是腰时，两腰和为6加上底边5，周长为11；②当5是腰时，两腰和为10加上底边3，周长为13.故选D. 如图，在△ABC中，BC=5cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是 cm．
5．
【解析】
试题分析：∵BP、CP分别是∠ABC和∠ACB的角平分线，∴∠ABP=∠PBD，∠ACP=∠PCE，∵PD∥AB，PE∥AC，∴∠ABP=∠BPD，∠ACP=∠CPE，∴∠PBD=∠BPD，∠PCE=∠CPE，∴BD=PD，CE=PE，∴△PDE的周长=PD+DE+PE=BD+DE+EC=BC=5cm．故答案为：5． 已知：△ABC中，∠B=90°， ∠A、∠C的平分线交于点O，则∠AOC的度数为
A. 60° B. 90° C. 45° D. 135°
D
【解析】
∵∠B=90°，
∴∠BCA+∠BAC=90°，
∵CD平分∠ACB，AE平分∠CAB，
∴∠OCA=∠BCA，∠OAC=∠BAC，
∴∠OCA+∠OAC=∠BCA+∠BAC=（∠BCA+∠BAC）=45°，
∴∠AOC=135°.
故选D. 三角形中到三边距离相等的点是（ ）
A. 三条边的中垂线交点 B. 三条高交点
C. 三条中线交点 D. 三条角平分线的交点
D
【解析】由角平分线的性质不难得出三角形中到三边距离相等的点是三条角平分线的交点.
故选D. （2b-2c）2等于_______；
4b2-8bc+4c2
【解析】根据完全平方公式可得：（2b-2c）2=4b2-8bc+4c2. （x+6y）（x-6y）等于（ ）
A. x2-6y 2 B. x2-y 2 C. x2-36y 2 D. 36x2-y 2
C
【解析】根据平方差公式可得：（x+6y）（x-6y）=x2-36y 2 ，故选C.