题目内容
到一个角的两边距离相等的点都在_________。
 这个角的平分线上
【解析】根据定义可知:到一个角的两边距离相等的点在这个角的平分线上、角平分线上的点到这个角的两边的距离相等。
这个角的平分线上
【解析】根据定义可知:到一个角的两边距离相等的点在这个角的平分线上、角平分线上的点到这个角的两边的距离相等。
练习册系列答案
相关题目
解方程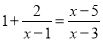 时,去分母得( )
时,去分母得( )
A. 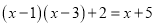 B.
B. 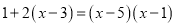
C. 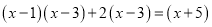 D.
D. 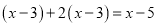
 C
【解析】观察可得最简公分母是(x-1)(x-3),方程两边都乘最简公分母,即可把分式方程转换为整式方程.
方程两边同乘(x-1)(x-3)得(x-1)(x-3)+2(x-3)=(x-5)(x-1),
故选C.
C
【解析】观察可得最简公分母是(x-1)(x-3),方程两边都乘最简公分母,即可把分式方程转换为整式方程.
方程两边同乘(x-1)(x-3)得(x-1)(x-3)+2(x-3)=(x-5)(x-1),
故选C. 等腰三角形的一个外角为110°,则底角的度数可能是_______.
 70°或55°
【解析】当110°是等腰三角形底角的外角时,底角为70°;当110°是等腰三角形顶角的外角时,因为等腰三角形两底角相等,所以一个底角的度数等于外角110°的一半,即55°.
70°或55°
【解析】当110°是等腰三角形底角的外角时,底角为70°;当110°是等腰三角形顶角的外角时,因为等腰三角形两底角相等,所以一个底角的度数等于外角110°的一半,即55°. 在△ABC中,AB=AC,BD是角平分线,BD=AD,求∠A的度数.
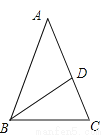
 ∠A=36°
【解析】试题分析:设∠A的度数为x°,由等腰三角形的性质分别表示出∠ABC和∠C的度数,再根据三角形内角和列方程求解即可.
试题解析:
设∠A=x°,
∵BD=AD,
∴∠A=∠ABD=x°,
∴∠BDC=∠A+∠ABD=2x°,
∵BD=BC,
∴∠BDC=∠BCD=2x°,
∵AB=AC,
∴∠ABC=∠BCD=2x°,...
∠A=36°
【解析】试题分析:设∠A的度数为x°,由等腰三角形的性质分别表示出∠ABC和∠C的度数,再根据三角形内角和列方程求解即可.
试题解析:
设∠A=x°,
∵BD=AD,
∴∠A=∠ABD=x°,
∴∠BDC=∠A+∠ABD=2x°,
∵BD=BC,
∴∠BDC=∠BCD=2x°,
∵AB=AC,
∴∠ABC=∠BCD=2x°,... 在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD∶CD=9∶7,则D到AB的距离为______
 18
【解析】试题分析:过点D作DE⊥AB,由BC=32,BD∶CD=9∶7,即可求得CD的长,再根据角平分线的性质即可求得结果.
过点D作DE⊥AB,
∵BD∶CD=9∶7,
∴CD=BC·=14
∵AD平分∠CAB,DE⊥AB,∠C=90°
∴DE=CD=14
18
【解析】试题分析:过点D作DE⊥AB,由BC=32,BD∶CD=9∶7,即可求得CD的长,再根据角平分线的性质即可求得结果.
过点D作DE⊥AB,
∵BD∶CD=9∶7,
∴CD=BC·=14
∵AD平分∠CAB,DE⊥AB,∠C=90°
∴DE=CD=14 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE+DE等于( )
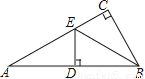
A. 2cm B. 3cm C. 4cm D. 5cm
 B
【解析】试题分析:根据角平分线的性质,由BE平分∠ABC,∠ACB=90°,DE⊥AB,可得CE=DE,即可求得结AE+DE=AE+CE=AC=3cm.
故选B.
B
【解析】试题分析:根据角平分线的性质,由BE平分∠ABC,∠ACB=90°,DE⊥AB,可得CE=DE,即可求得结AE+DE=AE+CE=AC=3cm.
故选B. 某超市购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个.如果超市将篮球售价定为x元(x>50),每月销售这种篮球获利y元.
(1)求y与x之间的函数关系式;
(2)超市计划下月销售这种篮球获利8000元,又要吸引更多的顾客,那么这种篮球的售价应定为多少元?
 (1) y=-10x2+1400x-40000,50<x<100;(2)60元.
【解析】试题分析:(1)根据利润问题的数量关系,利润=售价-进价就可以得出每个篮球的利润,设销售这批篮球的利润为y元,根据销售问题的数量关系表示出y与x之间的函数关系式;
(2)令函数值y=8000,求得合适的x的值即可.
试题解析:
【解析】
(1)由题意,篮球售价定为x元,得每个篮球所获...
(1) y=-10x2+1400x-40000,50<x<100;(2)60元.
【解析】试题分析:(1)根据利润问题的数量关系,利润=售价-进价就可以得出每个篮球的利润,设销售这批篮球的利润为y元,根据销售问题的数量关系表示出y与x之间的函数关系式;
(2)令函数值y=8000,求得合适的x的值即可.
试题解析:
【解析】
(1)由题意,篮球售价定为x元,得每个篮球所获... (x-2y)2等于_______;
 x2-8xy+4y2
【解析】根据完全平方公式可得:(x-2y)2=x2-8xy+4y2.
x2-8xy+4y2
【解析】根据完全平方公式可得:(x-2y)2=x2-8xy+4y2. (2x+1)(2x-1)等于( )
A. 4x2-1 B. 2x2-1 C. x2-1 D. 2x2+1
 A
【解析】根据平方差公式可得:(2x+1)(2x-1)=4x2-1,故选A.
A
【解析】根据平方差公式可得:(2x+1)(2x-1)=4x2-1,故选A. 
