题目内容
点O是△ABC内一点,且点O到三边的距离相等,∠A=60°,则∠BOC的度数为_______.
 120°
120°
练习册系列答案
相关题目
分式方程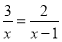 的解是( )
的解是( )
A. 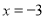 B.
B. 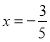 C.
C. 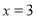 D. 无解
D. 无解
 C.
【解析】
试题分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
去分母得:3x-3=2x,
解得:x=3,
经检验x=3是分式方程的解.
故选C.
考点: 解分式方程.
C.
【解析】
试题分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
去分母得:3x-3=2x,
解得:x=3,
经检验x=3是分式方程的解.
故选C.
考点: 解分式方程. △ABC中,若∠A=80°,∠B=50°,AC=5,则AB= .
 5.
【解析】
试题解析:∵∠A=80°,∠B=50°,
∴∠C=180°-80°-50°=50°,
∴AB=AC=5.
5.
【解析】
试题解析:∵∠A=80°,∠B=50°,
∴∠C=180°-80°-50°=50°,
∴AB=AC=5. 等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )
A. 7 B. 11 C. 7或11 D. 7或10
 C
【解析】试题分析:题中给出了周长关系,要求底边长,首先应先想到等腰三角形的两腰相等,寻找问题中的等量关系,列方程求解,然后结合三角形三边关系验证答案.设等腰三角形的底边长为x,腰长为y,则根据题意,得①或②,解方程组①得:x=11,y=8,根据三角形三边关系定理,此时能组成三角形;解方程组②得:x=7,y=10,根据三角形三边关系定理此时能组成三角形,即等腰三角形的底边长是11或7.
...
C
【解析】试题分析:题中给出了周长关系,要求底边长,首先应先想到等腰三角形的两腰相等,寻找问题中的等量关系,列方程求解,然后结合三角形三边关系验证答案.设等腰三角形的底边长为x,腰长为y,则根据题意,得①或②,解方程组①得:x=11,y=8,根据三角形三边关系定理,此时能组成三角形;解方程组②得:x=7,y=10,根据三角形三边关系定理此时能组成三角形,即等腰三角形的底边长是11或7.
... 已知:AC=AD,AB是∠CAD的角平分线,求证:BC=BD.
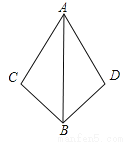
 证明见解析.
【解析】证明:∵AB是∠CAD的角平分线
∴∠BAC=∠BAD ……………………………………………1分
在△ABC和△ABD中
……………………………………3分
∴△ABC≌△ABD …………………………4分
∴BC=BD
证明见解析.
【解析】证明:∵AB是∠CAD的角平分线
∴∠BAC=∠BAD ……………………………………………1分
在△ABC和△ABD中
……………………………………3分
∴△ABC≌△ABD …………………………4分
∴BC=BD 三角形中∠B的平分线和外角的平分线的夹角是( ).
A. 60° B. 90° C. 45° D. 135°
 B
【解析】
如图,BD平分∠ABF,BE平分∠ABC,
∴∠ABD=∠ABF,∠ABE=∠ABC,
∴∠DBE=∠DBA+∠ABE=∠ABF+∠ABC=(∠ABF+∠ABC)=90°.
故选B.
B
【解析】
如图,BD平分∠ABF,BE平分∠ABC,
∴∠ABD=∠ABF,∠ABE=∠ABC,
∴∠DBE=∠DBA+∠ABE=∠ABF+∠ABC=(∠ABF+∠ABC)=90°.
故选B. 如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
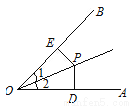
A. PD=PE B. OD=OE C. ∠DPO=∠EPO D. PD=OP
 D
【解析】试题分析:根据角平分线的性质可得:PD=PE,根据题意HL判定定理可得:Rt△POE≌Rt△POD,则OD=OE,∠DPO=∠EPO.
D
【解析】试题分析:根据角平分线的性质可得:PD=PE,根据题意HL判定定理可得:Rt△POE≌Rt△POD,则OD=OE,∠DPO=∠EPO. 982+(a-b)2
 9604+a2-2ab+b2
【解析】试题分析:把98化为(100-2),利用完全平方公式即可解答.
试题解析:
982+(a-b)2=(100-2)2+a2-2ab+b2=10000-400+4+a2-2ab+b2=9604+a2-2ab+b2.
9604+a2-2ab+b2
【解析】试题分析:把98化为(100-2),利用完全平方公式即可解答.
试题解析:
982+(a-b)2=(100-2)2+a2-2ab+b2=10000-400+4+a2-2ab+b2=9604+a2-2ab+b2. (2x+y 2 )(2x-y 2 )等于( )
A. x2-y 4 B. x2-y 2 C. 4x2-y4 D. 4x2-y 2
 C
【解析】根据平方差公式可得:(2x+y 2 )(2x-y 2 )=4x2-y4 ,故选C.
C
【解析】根据平方差公式可得:(2x+y 2 )(2x-y 2 )=4x2-y4 ,故选C.