在△ABC中，AB=BC，∠ABC=84°，BD是∠ABC的平分线，DE∥BC；求∠EDB的度数.
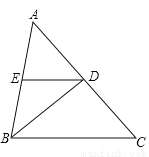
∠EDB=42°.
【解析】试题分析：因为BD是∠ABC的平分线，所以∠ABD=∠CBD，所以∠DBC=84°÷2=42°，因为DE∥BC，所以∠EDB=∠DBC=42°.
试题解析：
∵BD是∠ABC的平分线，
∴∠ABD=∠CBD，
∴∠DBC=84°÷2=42°，
∵DE∥BC，
∴∠EDB=∠DBC=42°. 如图，AB⊥AC，BF是∠ABC的平分线，若∠BFC=110°，求∠C的度数.
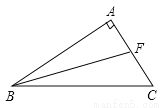
∠C=50°
【解析】试题分析：因为∠BFC=110°，根据三角形的外角等于不相邻的两个内角之和，可以得到∠ABF+∠A=110° ，所以∠ABF=110°－90°=20°，因为BF是∠ABC的角平分线，所以可以得到∠ABC=2∠ABF=40°，即在△ABC中∠C=180°－90°－40°=50°.
试题解析：
∵∠BFC=110°，
∴∠ABF=110°－90°=20°，... 在△ABC中，AB=AC，BD是角平分线，BD=AD，求∠A的度数．
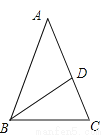
∠A=36°
【解析】试题分析：设∠A的度数为x°，由等腰三角形的性质分别表示出∠ABC和∠C的度数，再根据三角形内角和列方程求解即可.
试题解析：
设∠A=x°，
∵BD=AD，
∴∠A=∠ABD=x°，
∴∠BDC=∠A+∠ABD=2x°，
∵BD=BC，
∴∠BDC=∠BCD=2x°，
∵AB=AC，
∴∠ABC=∠BCD=2x°，... 已知：如图△ABC中，AB=AC，CD、BE是△ABC的角平分线.求证：AD=AE．
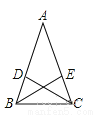
证明见解析.
【解析】试题分析：先根据CD、BE是△ABC的角平分线和等腰三角形的性质得到，∠1=∠2，∠A=∠A，结合AB=AC，可证△ADC≌△AEB，所以AD=AE．
试题解析：∵AB=AC（已知），
∴∠ABC=∠ACB．
∵CD、BE是△ABC的角平分线（已知），
∴∠1=∠ABC，∠2=∠ACB，
∴∠1=∠2．
又∵∠A=∠A（已知），
... 等腰三角形的一个角是80°，则它的顶角的度数是（ ）
A. 80° B. 80°或20° C. 80°或50° D. 20°
B
【解析】试题分析：分80°角是顶角与底角两种情况讨论求解． ①80°角是顶角时，三角形的顶角为80°，
②80°角是底角时，顶角为180°﹣80°×2=20°， 综上所述，该等腰三角形顶角的度数为80°或20°． 已知等腰三角形的两边长分别是3和5，则该三角形的周长是（ ）
A. 8 B. 9 C. 10或12 D. 11或13
D
【解析】分两种情况：①当3是腰时，两腰和为6加上底边5，周长为11；②当5是腰时，两腰和为10加上底边3，周长为13.故选D. 等腰△ABC中，AB=AC，一边上的中线BD将这个三角形的周长分为15和12两个部分，则这个等腰三角形的底边长为（ ）
A. 7 B. 11 C. 7或11 D. 7或10
C
【解析】试题分析：题中给出了周长关系，要求底边长，首先应先想到等腰三角形的两腰相等，寻找问题中的等量关系，列方程求解，然后结合三角形三边关系验证答案．设等腰三角形的底边长为x，腰长为y，则根据题意，得①或②，解方程组①得：x=11，y=8，根据三角形三边关系定理，此时能组成三角形；解方程组②得：x=7，y=10，根据三角形三边关系定理此时能组成三角形，即等腰三角形的底边长是11或7.
... 等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（ ）
A. 60° B. 120° C. 60°或150° D. 60°或120°
D
【解析】试题分析：等腰三角形的高相对于三角形有三种位置关系，三角形内部，三角形的外部，三角形的边上．根据条件可知第三种高在三角形的边上这种情况不成了，因而应分两种情况进行讨论．
【解析】
当高在三角形内部时（如图1），顶角是60°；
当高在三角形外部时（如图2），顶角是120°．
故选D． 如图，在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=72°，则∠ABD=（ ）
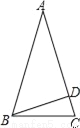
A. 36° B. 54° C. 18° D. 64°
B
【解析】试题分析：根据等腰三角形的性质由已知可求得∠A=36°，再根据垂直的定义和三角形内角和定理不难求得∠ABD=90°﹣36°=54°．
故选：B． 在△ABC中，D是BC上的点，AB=AD=DC，∠B=70°，则∠C的度数为（ ）
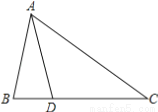
A. 35° B. 40° C. 45° D. 50°
A
【解析】∵AB=AD, ∴∠ADB=∠B=70°.
∵AD=DC，
∴35°.
故选A.