��Ŀ����
����������һ���ϵĸ�����һ���ļн�Ϊ30�㣬�ǵĶ���Ϊ�� ��
A. 60�� B. 120�� C. 60���150�� D. 60���120��
 D
��������������������������εĸ������������������λ�ù�ϵ���������ڲ��������ε��ⲿ�������εı��ϣ�����������֪�����ָ��������εı���������������ˣ����Ӧ����������������ۣ�
��������
�������������ڲ�ʱ����ͼ1����������60�㣻
�������������ⲿʱ����ͼ2����������120�㣮
��ѡD��
D
��������������������������εĸ������������������λ�ù�ϵ���������ڲ��������ε��ⲿ�������εı��ϣ�����������֪�����ָ��������εı���������������ˣ����Ӧ����������������ۣ�
��������
�������������ڲ�ʱ����ͼ1����������60�㣻
�������������ⲿʱ����ͼ2����������120�㣮
��ѡD��
��ϰ��ϵ�д�
 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�
�����Ŀ
�ⷽ��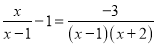
 ���������������۲�ɵ����ĸ��(x-1��(x+2),�������߳����ĸ,���ѷ�ʽ����ת��Ϊ��ʽ������⣻
�������������ͬʱ�����ĸ
������ʽ����Ϊ��
�����õ��� ���������Ƿ��̵Ľ�.
���������������۲�ɵ����ĸ��(x-1��(x+2),�������߳����ĸ,���ѷ�ʽ����ת��Ϊ��ʽ������⣻
�������������ͬʱ�����ĸ
������ʽ����Ϊ��
�����õ��� ���������Ƿ��̵Ľ�. ����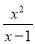 ��
��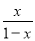 �Ľ����__����x��2ʱ��ԭʽ��ֵΪ__.
�Ľ����__����x��2ʱ��ԭʽ��ֵΪ__.
 x 2
�����������������
ԭʽ
��ʱ��ԭʽ
�ʴ�Ϊ��
x 2
�����������������
ԭʽ
��ʱ��ԭʽ
�ʴ�Ϊ�� ���������ε�һ�����Ϊ110�㣬��ǵĶ���������_______.
 70���55��
����������110���ǵ��������εǵ����ʱ����Ϊ70�㣻��110���ǵ��������ζ��ǵ����ʱ����Ϊ����������������ȣ�����һ���ǵĶ����������110���һ�룬��55��.
70���55��
����������110���ǵ��������εǵ����ʱ����Ϊ70�㣻��110���ǵ��������ζ��ǵ����ʱ����Ϊ����������������ȣ�����һ���ǵĶ����������110���һ�룬��55��. �ڵ�����ABC�У�AB=AC�����ܳ�Ϊ20cm����AB�ߵ�ȡֵ��Χ�ǣ� ��
A. 1cm��AB��4cm B. 5cm��AB��10cm
C. 4cm��AB��8cm D. 4cm��AB��10cm
 B
��������������������ڵ�����ABC�У�AB=AC�����ܳ�Ϊ20cm������AB="AC=x" cm����BC=��20��2x��cm���࣬���5cm��x��10cm����ѡB��
B
��������������������ڵ�����ABC�У�AB=AC�����ܳ�Ϊ20cm������AB="AC=x" cm����BC=��20��2x��cm���࣬���5cm��x��10cm����ѡB�� �ڡ�ABC�У�AB=AC��BD�ǽ�ƽ���ߣ�BD=AD�����A�Ķ�����
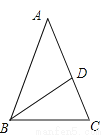
 ��A=36��
��������������������A�Ķ���Ϊx�㣬�ɵ��������ε����ʷֱ��ʾ����ABC�͡�C�Ķ������ٸ����������ڽǺ��з�����⼴��.
���������
���A=x�㣬
��BD=AD��
���A=��ABD=x�㣬
���BDC=��A+��ABD=2x�㣬
��BD=BC��
���BDC=��BCD=2x�㣬
��AB=AC��
���ABC=��BCD=2x�㣬...
��A=36��
��������������������A�Ķ���Ϊx�㣬�ɵ��������ε����ʷֱ��ʾ����ABC�͡�C�Ķ������ٸ����������ڽǺ��з�����⼴��.
���������
���A=x�㣬
��BD=AD��
���A=��ABD=x�㣬
���BDC=��A+��ABD=2x�㣬
��BD=BC��
���BDC=��BCD=2x�㣬
��AB=AC��
���ABC=��BCD=2x�㣬... �ڡ�ABC�У���C=90�㣬ADƽ�֡�BAC��BC��D����BC=32����BD��CD=9��7����D��AB�ľ���Ϊ______
 18
���������������������D��DE��AB����BC=32��BD��CD=9��7���������CD�ij����ٸ��ݽ�ƽ���ߵ����ʼ�����ý��.
����D��DE��AB��
��BD��CD=9��7��
��CD=BC��=14
��ADƽ�֡�CAB��DE��AB����C=90��
��DE=CD=14
18
���������������������D��DE��AB����BC=32��BD��CD=9��7���������CD�ij����ٸ��ݽ�ƽ���ߵ����ʼ�����ý��.
����D��DE��AB��
��BD��CD=9��7��
��CD=BC��=14
��ADƽ�֡�CAB��DE��AB����C=90��
��DE=CD=14 ij���й���һ�ֵ���Ϊ40Ԫ����������Ե���50Ԫ���ۣ���ôÿ�¿��۳�500�����������۾��飬�ۼ�ÿ���1Ԫ����������Ӧ����10����������н������ۼ۶�ΪxԪ(x��50)��ÿ�����������������yԪ��
(1)��y��x֮��ĺ�����ϵʽ��
(2)���мƻ��������������������8000Ԫ����Ҫ��������Ĺ˿ͣ���ô����������ۼ�Ӧ��Ϊ����Ԫ��
 (1) y����10x2��1400x��40000��50��x��100����2��60Ԫ.
�������������������1���������������������ϵ�������ۼۣ����۾Ϳ��Եó�ÿ������������������������������ΪyԪ���������������������ϵ��ʾ��y��x֮��ĺ�����ϵʽ��
��2�����ֵy��8000����ú��ʵ�x��ֵ���ɣ�
���������
��������
��1�������⣬�����ۼ۶�ΪxԪ����ÿ����������...
(1) y����10x2��1400x��40000��50��x��100����2��60Ԫ.
�������������������1���������������������ϵ�������ۼۣ����۾Ϳ��Եó�ÿ������������������������������ΪyԪ���������������������ϵ��ʾ��y��x֮��ĺ�����ϵʽ��
��2�����ֵy��8000����ú��ʵ�x��ֵ���ɣ�
���������
��������
��1�������⣬�����ۼ۶�ΪxԪ����ÿ����������... ��-a-b����a-b������_______��
 b2-a2
������������ƽ���ʽ�ɵã���-a-b����a-b��=b2-a2.
b2-a2
������������ƽ���ʽ�ɵã���-a-b����a-b��=b2-a2. 
