题目内容
已知等腰三角形的两边长分别是3和5，则该三角形的周长是（ ）
A. 8 B. 9 C. 10或12 D. 11或13
D
【解析】分两种情况：①当3是腰时，两腰和为6加上底边5，周长为11；②当5是腰时，两腰和为10加上底边3，周长为13.故选D.
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
分式方程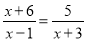
的最简公分母是___________
【解析】找最简公分母首先看相同的式子，并且式子的指数最高，本题中的最简公分母是(x-1)(x+3).故答案为：（x-1）(x+3). 计算：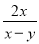 
＋
＝__
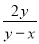2
【解析】试题解析：原式
故答案为：2. 已知△ABC中，三边a，b，c满足|b-c|+（a-b）2=0，则∠A等于（ ）
A. 60° B. 45° C. 90° D. 不能确定
A
【解析】△ABC中，三边a，b，c满足|b-c|+（a-b）2=0∴b-c=0，a-b=0，
∴a=b=c，
∴a=b=c，
∴三角形是等边三角形，
∴∠A=60°.
故选A. 如图，在△ABC中，∠B=∠C，AB=5，则AC的长为（ ）
A．2 B．3 C．4 D．5
D
【解析】
根据等腰三角形的性质可得AB=AC，继而得出AC的长．
【解析】
∵∠B=∠C，
∴AB=AC=5．
故选D． 在△ABC中，AB=BC，∠ABC=84°，BD是∠ABC的平分线，DE∥BC；求∠EDB的度数.
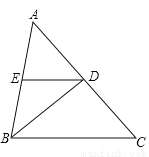
∠EDB=42°.
【解析】试题分析：因为BD是∠ABC的平分线，所以∠ABD=∠CBD，所以∠DBC=84°÷2=42°，因为DE∥BC，所以∠EDB=∠DBC=42°.
试题解析：
∵BD是∠ABC的平分线，
∴∠ABD=∠CBD，
∴∠DBC=84°÷2=42°，
∵DE∥BC，
∴∠EDB=∠DBC=42°. 三角形的三条角平分线相交于一点，并且这一点到________________相等
三边的距离
【解析】三角形三条角平分线的交点到三角形三条边的距离相等.
故答案为三边的距离. 某广告公司设计一幅周长为12m的矩形广告牌，广告设计费用为1000元/m2.设矩形的一边长为xm，面积为ym2.
(1)求出y与x之间的函数关系式，说明y是不是x的二次函数，并确定x的取值范围；
(2)若x＝3时，广告牌的面积最大，求此时的广告费应为多少？
(1)y＝－x2＋6x，是，0＜x＜6 ；（2）9000元
【解析】试题分析：
（1）矩形的一边长为xm，根据矩形的周长是12m，可得矩形的另一边长为（6－x）m，根据矩形的面积公式即可得出y与x之间的函数表达式；
（2）把x＝3代入函数的解析式得出y的值即为广告牌的最大面积，再乘以1000即为此时的广告费．
试题解析：
【解析】
（1）由题意得出：y ＝x(6－x... （5+x2）（5-x2）等于_______；
25-x4
【解析】根据平方差公式可得：（5-x2）（5-x2）=25-x4.